|
Numbered among the great |
| Above: the transition from an Earth-centred view of the Universe (left) to a Suncentred view (right) was made largely on grounds of mathematical elegance and harmony. The ancient system worked well (despite the dejected appearance of the ancient astronomers depicted at the foot of this map, drawn in 1660). Yet many of the most able scientists accepted the arguments of Copernicus for the mathematically simpler Sun-centred system, even before telescopic evidence supported the theory | |
Number lies behind scientific theory, ideas of artistic proportion and rules of musical harmony. HILDI HAWKINS shows how artists and scientists have seen meaning in number, and how patterns of numbers have guided them in their creative work
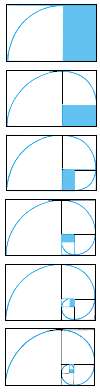
| Above: cutting a square from a rectangle with sides in the ratio of the golden section (1.618) leaves a smaller 'golden' rectangle. Repeated, this creates a Fibonacci spiral, which is common in nature (below) |
 |
THE BELIEF THAT NUMBER is the key to the secrets of the Universe- a belief verging on the mystical - lay at the heart of many arts and branches of learning up to, and even after, the scientific revolution of the 17th century. It was the inspiration for some of their most spectacular achievements. Diverse disciplines were brought together by the common language of number: music, astronomy, architecture, poetry and theology reflected the harmonia mundi, the harmony of the world, by means of number.
Number was in everything; a typical
expression of this idea is St Augustine's remark
on dancing:
Ask what delights you in dancing and number will reply, 'Lo here am I!' Examine
the beauty of
bodily form, and you will find that everything is in its place by number.
Examine the beauty of bodily motion, and you will find everything in its
due time by number.
Number was the essence of the harmonia
mundi. And so the way to create a perfect work of art was to use number
in the correct way. This belief can be traced to
Plato, who states in his philosophical dialogue
Philebus:
'The qualities of measure and proportion invariably . . . constitute beauty
and elegance.'
The architect Leon Battista Alberti, writing in the mid 15th century, echoes
the idea:
Nature is sure to act consistently, and with a constant Analogy in all her
operations: from whence I conclude, that the same Numbers, by means of which
the Agreement of Sounds affects our ears with
delight, are the very same which please our eyes and minds.
The large number of handbooks on architectural proportion that
appeared during the Renaissance are testimony to the seriousness with which
this idea was regarded. And in the 20th century a major attempt at constructing
a harmonious system of design by proportion was made by the great architect
Le Corbusier.
Called the Modulor, Corbusier's system was based on the
golden section, a ratio regarded since ancient
times as especially pleasing. If a line is divided into unequal parts in
such a way that the ratio of the whole to the longer part equals the ratio
of the longer part to the shorter, the line is said to be divided in golden
section. This ratio is called by the Greek letter
'phi'. It is approximately equal to 1.618. If
this number is repeatedly multiplied by itself, a series of numbers is formed,
everv member of which (after the first two) is equal to the sum of the preceding
two numbers.
A simpler example of such a series they
are called Fibonacci series after Leonardo
Fibonacci, a mathematician who worked in Pisa about 1200 - is the sequence:
1, 2, 3, 5, 8.... Fibonacci series are found in the proportions and ratios
of many natural patterns: the pads on a cat's foot, the arrangement of leaves
on a plant, the spirals of a snail's shell.
Building by numbers
Corbusier claimed that the proportions of ideal human figures embodied the
golden section, and that buildings designed in accordance with it would be
both beautiful and well-adapted to human needs. He designed several buildings
using the Fibonacci series, based on the figure of a man 6 feet (1.8 metres)
tall. He even believed that his system had reconciled
the metric and imperial systems of units. The buildings based on the
Modulor include the chapel at Ronchamp, in France, blocks of flats in many
famous cities, and the administrative centre at Chandigarh, in the Punjab.
 |
Left: a rare instance of a painting
deliberately designed using the golden section: The parade, by Seurat. The
ratios of the dimensions indicated are all approximately 1.618:1 |
Are these buildings more beautiful than others not constructed
on any particular system of proportion? The question is almost impossible
to answer, since the buildings named are the work of a great architect and,
as such, are likely to be better than those of an indifferent architect,
whether designed according to a system or not.
It is even doubtful that the golden section leads to more beautiful
proportions than any other ratio. A rectangle with length and breadth in
the ratio of the golden section has long been regarded as in some sense ideal.
Yet as long ago as 1876 it was found by experiment that, although subjects
preferred golden-section rectangles in the laboratory (35 per cent chose
them when offered a choice of 10 rectangles), a much shorter rectangle was
preferred for pictures in a gallery - 5:4 for upright shapes 4:3 for horizontal.
If it were the case that certain proportions were preferred, then, as the
architectural writer P. H. Scholfield points out:
One would expect the same types of relationships to have appeared spontaneously
in all periods of good design. In fact, this is not the case, and the sorts
of mathematical relationships which occur are closely related to the mathematical
knowledge of the period.
What role is played by number relationships
in science? The idea that there was an underlying numerical harmony in the
world made it natural for the ancients to seek scientific explanations in
terms of number. Reasoning of this sort led them to think that God must have
made the world in six days because six is the first
'perfect' number - a number equal
to the sum of its factors (see page
1326).
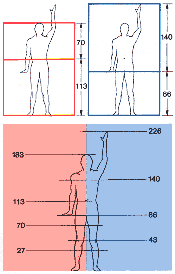
| The golden section, which fascinated Le
Corbusier, occurs repeatedly in the windows and recesses of his chapel at
Ronchamp (above). His Modulor system was based on a man 6 feet (183 centimetres)
tall. In the 'red' series this height is divided in golden section by the
height of the navel. The 'blue' series is based on the height of the raised
hand, above the ground and above the groin. Dividing these distances (shown
here in centimetres) by the golden section extends the two series (right),
which are related to basic human postures (below) |
 |
Today it seems that such an argument has no validity whatever. Yet it is undeniable that important discoveries have been made when numerical patterns have been noticed in natural phenomena, even if explanations for those patterns were still unknown. An example is the Titius-Bode 'law'. which led to the discovery of the asteroids. It was noticed that the relative distances of the planets from the Sun fall roughly into a sequence of numbers generated by a simple rule (see page 341). |
|
 |
||||
But there is a gap in the series, between Mars and Jupiter. It was argued
that there should be a planet at the corresponding position. A search was
made, and an object was indeed found there. It was not a planet but the first
known asteroid - a small rocky body, one of thousands that are now known.
| Below: Dmitri Mendeleev, the Russian chemist whose classification of the elements on the basis of their atomic weights underlies modern chemistry |
 |
Another example of scientific discovery guided by numerical patterns comes from chemistry. In the 19th century the Russian chemist Dmitri Mendeleev noticed that when the elements are listed in order of their atomic weights (which are literally, the relative weights of their atoms), patterns emerge: the list can be arranged in rows and columns so that the chemical properties change systematically along the rows and down the columns. To make this system work, it was sometimes necessarv to revise the atomic weights assigned to certain elements, or to suppose that there were gaps, corresponding to as yet undiscovered elements. Subsequent discoveries vindicated Mendeleev's ideas triumphantly. All known elements fit neatly into this 'periodic' table, and modern knowledge of atomic structure explains why these patterns should exist.
The modern view
The modern attitude to such numerical relationships among phenomena, empirically
found, is very different from that which was prevalent as late as the 18th
century. We see them as the inevitable product of relatively simple physical
laws: ancient philosophers and scientists, not knowing their explanations,
saw every such instance of regularity as another proof of the harmonious
and beautiful design of the world.
The desire to see the world as a place ruled by harmony and
governed by number may seem naïve today, but it is an expression ofthe
perennial tendency - and desire - of human beings to see order and pattern
in everything around them. Number may not be everything, but the unprovable
assumption that nature is rational and intelligible is the basis of science
- and of the practical reasoning of everyday life.
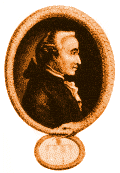 |
| Above: Immanuel Kant believed the mathematical
regularities of the world to be, in some sense, created by the human mind |
A radical attempt to account for this
intelligibility of the Universe was made by the German philosopher
Immanuel Kant in the 18th century.
He saw the source of the orderliness of the world as
being the human mind itself, and the concepts with which it does its thinking.
He went so far as to say: 'Our intellect does not draw its laws from nature
. . . but imposes them on nature.' Cause and
effect, time and
space, the laws of
mathematics and logic,
are the result of the constitution of our minds.
Sir Arthur
Eddington, an English astronomer, pushed a form of this idea even further
in the early 20th century. He believed that many highly detailed facts about
the Universe - namely, the value of certain numerical
constants - could be calculated without any appeal to experiment or
observation, but by pure mathematics alone.
But very few scientists and philosophers have accepted this view. The specific
features of the Universe are not to be explained by reference to the structure
of the human mind: and only experience can show which theories are actually
true of the world. It is therefore highly remarkable that the Universe should
prove to obey laws that are in fact simple, and harmonious.
Even more remarkable: nature has (so far) proved to be not only
intelligible by rational laws but intelligible in a way that is frequently
elegant and even beautiful. When Copernicus put forward his idea that the
Earth revolved around the Sun, rather than vice versa, it was not so much
the experimental evidence as the theory's elegance, or aesthetic appeal,
that was persuasive to contemporary thinkers.
Similarly, Einstein developed the
theory of relativity on the premise that 'absolute'
motion does not exist; that is, there can be no justification for saying
that, of two scientific observers moving relatively to each other, one is
'really' at rest and the other is not. There is no absolute standard of rest
in the Universe. Einstein was very little influenced by the problems raised
by such experiments as that of Michelson
and Morley (see page 803). The elegance and intrinsic power of
the theory played a large part in the theory's quick acceptance and the
conviction of scientists that it must be true.
That the laws of nature should be not only rational but elegant
seems almost too much to expect. Yet this astonishing metaphysical hypothesis
is constantly being borne out by science. Time and again physical reality
is found to coincide with the speculations of scientists, evolved from a
few basic facts and couched in the subtle language of mathematics. The
existence of many
subatomic particles has been suggested by 'gaps' in mathematical patterns
somewhat analogous to Mendeleev's table of the elements.
The branch of mathematics responsible for these achievements,
called 'group theory', was evolved between the
World wars as part of purely abstract algebra; yet it seemed tailor-made
for the understanding of particles that were to be discovered decades later.
In view of these amazing anticipations of experimental results
by the mathematical speculations of theoretical physicists, how does modern
science differ from numerology? It differs
in that it makes no assumptions about
the symbolic
meaning of numbers: numbers do not give insight into some divine master
plan of the Universe. But the assumption on which science rests - that
nature is regular and comprehensible by human reason - is every bit as mystical
as the idea that 'number is all'.
Music of the Spheres |
|
 |
The work of the great astronomer
Johannes Kepler (1571-1630) shows a curious fusion
of numerological and scientific thought. It was Kepler who formulated the
extraordinarily elegant laws that govern planetary motion. This man one of
the first great modern scientists, was also a profound mystic. Like Pythagoras and Plato, Kepler believed that the world was ruled by number. He tried hard to prove that the distances of the planets from the Sun were given by an arrangement of Euclid's five regular solids (left); by doing so, he believed, he could demonstrate something of the order of the mind of God. But his faith in number went further: he believed that musical harmony, mathematically expressed, and the harmony of the spheres were one and the same thing: 'I affirm and demonstrate that the movements [of the planets] are modulated according to harmonic proportions.' |
| Kepler could not resist pushing his theory further.
Each planet, he believed, sings a characteristic tune - and, by a calculation
involving the angle it describes in a day, as seen from the Sun, he was able
to work out what the tune for each planet was. The Earth sings a simple little
ditty - mi fa mi - indicating, Kepler asserted, that 'in this our domicile
misery and famine obtain.' |
|
| Further reading Christopher Butler, Number
symbolism, Routledge & Kegan Paul 1970 Richard Cavendish, The black art's, Routledge & Kegan Paul 1967 Morris Kline, Mathematics in western culture, Penguin 1972 |