|
|
|
|
|
|
|
|
|
The Nature of Space and Time
Two relativists present their distinctive views on the universe, its evolution
and the impact of quantum theory.
by Stephen W. Hawking and Roger Penrose
In 1994 Stephen W. Hawking and Roger
Penrose gave a series of public lectures on general
relativity at the lsaac Newton Institute for Mathematical Sciences at the
University of Cambridge. From these lectures, published this year by Princeton
University Press as The Nature of Space and Time,
SCIENTIFIC AMERICAN has culled excerpts
that serve to compare and contrast the perspectives of the two scientists.
Although they share a common heritage in physics- Penrose served on Hawking's
Ph.D. thesis committee at Cambridge-the lecturers differ in their vision
of quantum mechanics and its impact on the evolution of the universe. In
particular, Hawking and Penrose disagree on what happens to the information
stored in a
black
hole and on why the beginning of the universe differs from the end.
One of Hawking's major discoveries, made In 1973, was that quantum effects
will cause black holes to emit particles. The black hole will evaporate in
the process, so that ultimately perhaps nothing of the original mass will
be left. But during their formation, black holes swallow a lot of data-the
types, properties and configurations of the particles that fall in. Although
quantum theory requires that such information must be conserved, what finally
happens to it remains a topic of contentious debate.
Hawking and Penrose
both believe that when a black hole radiates, it loses the information it
held. But Hawking insists that the loss is irretrievable, whereas Penrose
argues that the loss is balanced by spontaneous measurements of quantum states
that introduce information back into the system.
Both scientists agree that a future quantum theory of gravity is needed to
describe nature. But they differ in their view of some aspects of this theory.
Penrose thinks that even though the fundamental forces of particle physics
are symmetric in time-unchanged if time is reversed-quantum gravity will
violate time symmetry. The time asymmetry will then explain why in the beginning
the universe was so uniform, as evinced by the microwave background radiation
left over from the big bang, whereas the end of the universe must be messy.
Penrose attempts to encapsulate this time asymmetry in his Weyl curvature
hypothesis. Space-time,as Albert Einstein discovered, is curved by the presence
of matter. But space- time can also have some intrinsic bending, a quantity
designated by the Weyl curvature. Gravitational waves and black holes, for
example, allow space-time to curve even in regions that are empty. In the
early universe the Weyl curvature was probably zero, but in a dying universe
the large number of black holes, Penrose argues, will give rise to a high
Weyl curvature. This property will distinguish the end of the universe from
the beginning. Hawking agrees that the big bang and the final "big crunch"
will be different, but he does not subscribe to a time asymmetry in the laws
of nature. The underlying reason for the difference, he thinks, is the way
in which the universes evolution is programmed. He postulates a kind of
democracy, stating that no point in the universe can be special; therefore,
the universe cannot have a boundary. This no-boundary proposal, Hawking claims,
explains the uniformity in the microwave background radiation. The physicists
diverge, ultimately, in their interpretation of quantum mechanics. Hawking
believes that all a theory has to do is provide predictions that agree with
data. Penrose thinks that simply comparing predictions with experiments is
not enough to explain reality. He points out that quantum theory requires
wave functions to be "superposed," a concept that can lead to absurdities.
The scientists thus pick up the threads of the famous debates between
Einstein and Niels Bohr
on the bizarre implications of quantum theory. -The Editors
|
Stephen Hawking on quantum black holes:
The quantum theory of black holes...seems to lead to a new level of
unpredictability in physics over and above the usual uncertainty associated
with quantum mechanics. This is because black holes appear to have
intrinsic entropy and to
lose information from our region of the universe. I should say that these
claims are controversial: many people working or quantum gravity, including
almost all those who entered it from particle physics, would instinctively
reject the idea that information about the quantum state of a system could
be lost However, they have had very little success in showing how information
can get out of a black hole. Eventually I believe they will be forced to
accept my suggestion that it is lost, just as they were forced to agree that
black holes radiate, which went against all their preconceptions ... The
fact that gravity is attractive means that it will tend to draw the matter
in the universe together to form objects like stars and galaxies. These can
support themselves for a time against further contraction by thermal pressure,
in the case of stars, or by rotation and internal motions, in the case of
galaxies. However, eventually the heat or the angular momentum will be carried
away and the object will begin to shrink. If the mass is less than about
one and a half times that of the Sun, the contraction can be stopped by the
degeneracy pressure of electrons or neutrons. The object will
settle down to be a white dwarf or a neutron star, respectively. However,
if the mass is greater than this limit there is nothing that can hold it
up and stop it continuing to contract. |
DEGENERACY PRESSURE
No two electrons or neutrons can occupy the same quantum state. Thus,when
any collection of these particles is squeezed into a small volume, those
in the highest quantum states become very energetic. The system then resists
further compression, exerting an outward push called degeneracy pressure.
|
Once it has shrunk to a certain critical size the gravitational
field of its surface will he so strong that the light cones
will be bent inward. You can see that even the outgoing light rays are bent
toward each other and so are converging rather than diverging. This means
that there is a closed trapped surface.... Thus there must be a region of
space-time from which it is not possible to escape to infinity. This region
is said to he a black hole. Its boundary is called the event horizon and
is a null surface formed by the light rays that just fail to
get away to infinity....
[A] large amount of information is lost when a body collapses to form a black
hole. The collapsing body is described by a very large number of parameters.
There are the types of matter and the multipole moments of
the mass distribution. Yet the black hole that forms is completely independent
of the type of matter and rapidly loses all the multipole moments except
the first two: the monopole moment, which is the mass,and the dipole moment,
which is the angular momentum. This loss of information didn't really matter
in the classical theory. One could say that all the information about the
collapsing body was still inside the black hole. It would be very difficult
for an observer outside the black hole to determine what the collapsing body
was like. However, in the classical theory it was still possible in principle.
The observer would never actually lose sight of the collapsing body. Instead
it would appear to slow down and get very dim as it approached the event
horizon. But the observer could still see what it was made of and how the
mass was distributed. However, quantum theory changed all this. First, the
collapsing body would send out only a limited number of photons before it
crossed the event horizon. They would be quite insufficient to carry all
the information about the collapsing body. This means that in quantum theory
there's no way an outside observer can measure the state of the collapsed
body. One might not think that this mattered too much, because the information
would still be inside the black hole even if one couldn't measure it from
the outside. But this is where the second effect of quantum theory on black
holes comes in .... [Quantum] theory will cause black holes to radiate and
lose mass. It seems that they will eventually disappear completely, taking
with them the information inside them. I will give arguments that this
information really is lost and doesn't come back in some form. As I will
show, this loss of information would introduce a new level of uncertainty
into physics over and above the usual uncertainty associated with quantum
theory. Unfortunately,
Heisenberg's uncertainty
principle, this extra level will he rather difficult to confirm
experimentally in the case of black holes.
Roger Penrose on quantum theory and space-time:
The great physical theories of the 20th century have been quantum theory,
special relativity, general relativity and quantum field theory. These theories
are not independent of each other: general relativity was built on special
relativity, and quantum field theory has special relativity and quantum theory
as inputs. It has been said that quantum field theory is the most accurate
physical theory ever, being accurate to about one part in about
1011. However, I would like to point out that general relativity
has, in a certain clear sense, now been tested to be correct to one part
in 1014 and this accuracy has apparently been limited merely by
the accuracy of clocks on Earth). I am speaking of the Hulse-Taylor binary
pulsar PSR 1913 + 16,a pair of neutron stars orbiting each
other, one of which is a pulsar. General relativity predicts that this orbit
will slowly decay (and the period shorten) because energy is lost through
the emission of gravitational waves. |
 |
| LIGHT CONES To depict space-time, physicists routinely
plot time on a vertical axis and space on a horizontal. In this scheme, light
rays emanating from any point in space fan out along the surface of a vertical
cone. Because no physical signal can cover more distance in a given time
than light can,any signals originating at that point are confined within
the volume of the light cone. |
| NULL SURFACE A surface in space along which light
travels is known as a null surface. The null surface surrounding a black
hole, called an event horizon, has the shape of a spherical shell. Nothing
that falls inside the event horizon can come back out. |
| MULTIPOLE MOMENTS The dynamics of an object can
be summarized by determining its multipole moments. Each moment is calculated
by dividing an object into tiny elements, multiplying the mass of each element
by its distance from the center zero, one or more times, then adding these
terms for all the elements. A sphere, for example, has a monopole moment,whereas
a dumbbell has a dipole moment, which allows it to acquire angular momentum
easily. |
 |
| PULSARS Some dying suns collapse into neutron stars,
massive objects made entirely of densely packed neutrons. Rapidly rotating
neutron stars become pulsars, so called because they emit pulses of
electromagnetic radiation at astonishingly regular millisecond - to-second
intervals. A pulsar sometimes orbits another neutron star, forming a binary
pair. |
|
This has indeed been observed, and the entire description
of the motion...agrees with general relativity (which I am taking to
include Newtonian theory)
to the remarkable accuracy, noted above, over an accumulated period of 20
years. The discoverers of this system have now rightly been awarded Nobel
Prizes for their work. The quantum theorists have always claimed that because
of the accuracy of their theory, it should be general relativity that is
changed to fit their mould, but I think now that it is quantum field theory
that has some catching up to do. Although these four theories have been
remarkably successful, they are not without their problems....General relativity
predicts the existence of space-time singularities. In quantum
theory there is the "measurement problem"-I shall describe this later. It
may be taken that the solution to the various problems of these theories
lies in the fact that they are incomplete on their own. For example,it is
anticipated by many that quantum field theory might "smear" out the singularities
of general relativity in some way....
I should now like to talk about information loss in black holes, which I
claim is relevant to this last issue. I agree with nearly all that Stephen
had to say on this. But while Stephen regards the information loss due to
black holes as an extra uncertainty in physics,above and beyond the uncertainty
from quantum theory, I regard it as a complementary" uncertainty.... It is
possible that a little bit of information escapes at the moment of the black
hole evaporation... but this tiny information gain will be much smaller than
the information loss in the collapse (in what I regard as any reasonable
picture of the hole's final disappearance).
If we enclose the system in a vast box, as a thought experiment, we can consider
the phase-space evolution of matter inside the box. In the region
of phase space corresponding to situations
in which a black hole is present, trajectories of physical evolution will
converge and volumes following these trajectories will shrink. This is due
to the information lost into the singularity in the black hole. This shrinking
is in direct contradiction to the theorem in classical mechanics, called
Liouville's Theorem, which says that volumes in phase space remain constant....
Thus a black hole space-time violates this conservation. However, in my picture,
this loss of phase- space volume is balanced by a process of "spontaneous"
quantum measurement in which information is gained and phase-space volumes
increase. This is why I regard the uncertainty due to information loss in
black holes as being "complementary" to the uncertainty in quantum theory:
one is the other side of the coin to the other....
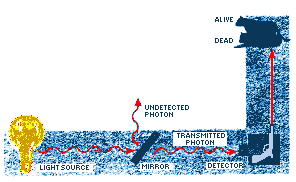
[Let] us consider the Schrödinger's cat thought experiment.
It describes the plight of a cat in a box, where (let us say) a photon is
emitted which encounters a half-silvered mirror, and the transmitted part
of the photon's wave function encounters a detector which, if it detects
the photon, automatically fires a gun, killing the cat. If it fails to detect
the photon, then the cat is alive and well. |
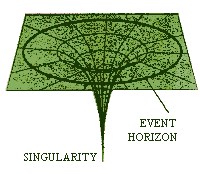 |
| SINGULARITIES According to general relativity,
under certain extreme conditions some regions of space-time develop infinitely
large curvatures, thus becoming singularities where the normal laws of physics
break down. Black holes, for example,should contain singularities hidden
inside the event horizon. |
| PHASE SPACE A
phase-space diagram is a mathematical
volume of many dimensions formed when coordinate axes are assigned to each
of the distance and momentum values of each particle. The motion of a group
of particles can then be represented by a moving element of volume in phase
space. |
| SCHRÖDINGER'S CAT Penrose invokes a thought
experiment originally invented by Einstein and used
by Erwin Schrödinger
to study the conceptual knots tied by wave functions. Prior to a measurement,
a system is assumed to be in a "
superposition" of quantum states
or waves, so that the value of, say, the momentum is uncertain. After a
measurement, the value of a quantity becomes known, and the system suddenly
assumes the one state that corresponds to the result. The significance of
the original superposition and the process by which the system "collapses"
into one state are highlighted by Schrödinger's cat paradox. |
|
(I know Stephen does not approve of mistreating cats, even
in a thought experiment! ) The wave function of the system is a superposition
of these two possibilities....But why does our perception not allow us to
perceive
macroscopic superpositions, of states
such as these, and not just the macroscopic alternatives "cat is dead" and
"cat is alive"... |
|
I am suggesting that something goes wrong with superpositions
of the alternative space-time geometries that would occur when general relativity
begins to become involved.
Perhaps a superposition of two different geometries is unstable and decays
into one of the two alternatives. For example, the geometries might be the
space-times of a live cat, or a dead one. I call this decay into one or the
other alternative objective reduction, which I like as a name because it
has an appropriately nice acronym (OR). How does the
Planck length 10-33 centimeter relate
to this? Nature's criterion for determining when two geometries are significantly
different would depend upon the Planck scale, and this fixes
the timescale in which the reduction into different alternatives occurs.
Hawking on quantum cosmology:
I will end this lecture on a topic on which Roger and I have very different
views-the arrow of time. There is a very clear distinction between the forward
and the backward directions of time in our region of the universe. One only
has to watch a film being run backward to see the difference. Instead of
cups falling off tables and getting broken, they would mend themselves and
jump back on the table. If only real life were like that. The local laws
that physical fields obey are time symmetric, or more precisely, CPT
(charge-parity-time) invariant. Thus, the observed difference between
the past and the future must come from the boundary conditions of the universe.
Let us take it that the universe is spatially closed and that it expands
to a maximum size and collapses again. As Roger has emphasized, the universe
will be very different at the two ends of this history. At what we call the
beginning of the universe, it seems to have been very smooth and regular.
However, when it collapses again, we expect it to be very disordered and
irregular. Because there are so many more disordered configurations than
ordered ones, this means that the initial conditions would have had to be
chosen incredibly precisely. It seems, therefore, that there must be different
boundary conditions at the two ends of time. Roger's proposal is that the
Weyl tensor should vanish at one end of time but not the other.
The Weyl tensor is that part of the curvature of space-time that is not locally
determined by the matter through the Einstein equations. It would have been
small in the smooth, ordered early stages but large in the collapsing universe.
Thus, this proposal would distinguish the two ends of time and so might explain
the arrow of time.
I think Roger's proposal is Weyl in more than one sense of the word. First,
it is not CPT invariant. Roger sees this as a virtue, but I feel one should
hang on to symmetries unless there are compelling reasons to give them up.
Second, if the Weyl tensor had been exactly zero in the early universe, it
would have been exactly homogeneous and isotropic - and would have remained
so for all time. Roger's Weyl hypothesis could not explain the fluctuations
in the background nor the perturbations that give rise to galaxies and bodies
like ourselves. Despite all this, I think Roger has put his finger on an
important difference between the two ends of time. But the fact that the
Weyl tensor was small at one end should not be imposed as an ad hoc boundary
condition but should be deduced from a more fundamental principle, the
no-boundary proposal....
How can the two ends of time be different? Why should perturbations be small
at one end but not the other? The reason is there are two possible complex
solutions of the field equations.... Obviously, one solution corresponds
to one end of time and the other to the other.... At one end,the universe
was very smooth and the Weyl tensor was very small. It could not, however
be exactly zero, for that would have been a violation of the uncertainty
principle. Instead there would have been small fluctuations that later grew
into galaxies and bodies like us. By contrast, the universe would have been
very irregular and chaotic at the other end of time with a Weyl tensor that
was typically large. This would explain the observed arrow of time and why
cups fall off tables and break rather than mend themselves and jump back
on. |
| PLANCK SCALE The Planck scale is an unattainably
small distance-related, by quantum mechanics, to an impossibly small time
span and high energy-that emerges when the fundamental constants for
gravitational attraction, the velocity of light and quantum mechanics are
appropriately combined. The scale represents the distance or energy at which
current concepts of space, time and matter break down, and a future theory,
quantum gravity,presumably takes over. |
 |
| CPT (CHARGE-PARITY-TIME) INVARIANCE This powerful
principle requires that theories describing particles must remain true even
when the charge, parity (or handedness) and time simultaneously reverse.
In other words, the behavior of a negatively charged electron with clockwise
spin moving forward in time must be identical to that of a positively charged
positron with anticlockwise spin moving backward in time. |
| WEYL TENSOR The curvature of space-time has two
components. One derives from the presence of matter in space-time; the other,
recognized by the German mathematician Hermann Weyl , occurs even in the
absence of matter. The mathematical quantity that describes this curvature
is called the Weyl tensor. |
 |
| NO-BOUNDARY PROPOSAL Hawking suggests that the evolution
of the universe Is explained by the no-boundary proposal, put forth in 1983
by him and James B. Hartle of the University of California at Santa Barbara.
The idea that the universe has no boundary places constraints on how the
equations of cosmology ere solved. Hawking believes these conditions will
lead to the ends of the universe being different, thereby determining the
direction of time's arrow. |
|
Penrose on quantum cosmology:
From what I understand of Stephen's position, I don't think that our disagreement
is very great on this point [the Weyl curvature hypothesis].
For an initial singularity the Weyl curvature is approximately zero.... Stephen
argued that there must be small quantum fluctuations in the initial state
and thus pointed out that the hypothesis that the initial Weyl curvature
is zero at the initial singularity is classical, and there is certainly some
flexibility as to the precise statement of the hypothesis. Small perturbations
are acceptable from my point of view, certainly in the quantum regime. We
just need something to constrain it very near to zero.... Maybe the no-boundary
proposal of [ James B.] Hartle and Hawking is a good candidate for the structure
of the initial state. However, it seems to me that we need something very
different to cope with the final state. In particular, a theory that explains
the structure of singularities would have to violate [CPT and other symmetries]
in order that something of the nature of the Weyl curvature hypothesis can
arise. This failure of time-symmetry might be quite subtle; it would have
to be implicit in the rules of that theory which goes beyond quantum
mechanics.
Hawking on physics and reality:
These lectures have shown very clearly the difference between Roger and me.
He's a Platonist and I'm
a positivist. He's worried that Schrödinger's cat is in a quantum state,
where it is half alive and half dead. He feels that can't correspond to reality.
But that doesn't bother me. I don't demand that a theory correspond to reality
because I don't know what it is. Reality is not a quality you can test with
litmus paper. All I'm concerned with is that the theory should predict the
results of measurements. Quantum theory does this very successfully.... Roger
feels that...the collapse of the wave function introduces CPT violation into
physics. He sees such violations at work in at least two situations: cosmology
and black holes. I agree that we may introduce time asymmetry in the way
we ask questions about observations. But I totally reject the idea that there
is some physical process that corresponds to the reduction of the wave function
or that this has anything to do with quantum gravity or consciousness. That
sounds like magic to me, not science.
|
 |
| WEYL CURVATURE HYPOTHESIS The universe Just after
the big bang has a small Weyl curvature, whereas near the end of time it
has a large Weyl curvature. Penrose suggests that this curvature, therefore,
accounts for the direction in which the arrow of time points. |
 |
Neils Bohr and Albert Einstein |
|
Penrose on physics and reality:
Quantum mechanics has only been around for 75 years. This is not very long
if one compares it, for example, with Newton's
theory of gravity. Therefore it wouldn't surprise me if quantum mechanics
will have to be modified for very macroscopic objects. At the beginning of
this debate, Stephen said that he thinks that he is a positivist, whereas
I am a Platonist. I am happy with him being a positivist, but I think that
the crucial point here is, rather, that I am a realist. Also, if one compares
this debate with the famous debate of Bohr and Einstein, some
70 years ago, I should think that Stephen plays the role of Bohr whereas
I play Einstein's role! For Einstein argued that there should exist something
like a real world, not necessarily represented by a wave function, whereas
Bohr stressed that the wave function doesn't describe a "real" microworld
but only "knowledge" useful for making predictions. Bohr was perceived to
have won the argument. In fact, according to the recent biography of Einstein
by [Abraham] Pais, Einstein might as well have gone fishing from 1925 onward.
Indeed, it is true that he didn't make many big advances, even though his
penetrating criticisms were very useful. I believe that the reason why Einstein
didn't continue to make big advances in quantum theory was that a crucial
ingredient was missing from quantum theory. This missing ingredient was Stephen's
discovery, 50 years later, of black hole radiation. It is this information
loss, connected with black hole radiation, which provides the new twist.
|
|
|
|
|
|
|
|
|
|
|