Maps that shape the world

"We wanted the computer to do absolutely as much as possible unassisted,but in no way violating the integrity of the aesthetics with which a human would have done it" - Mitchell Feigenbaum

Like a huge piece of orange peel that refuses to be flattened without tearing at the edges, the globe cannot be forced into two dimensions without distortion. But that distortion can now be minimised

Ian Mundell

IN 1940 the US Air Force estimated that less than 10 per cent of the world was mapped in enough detail to make the charts its pilots needed. Aerial surveying during and after the Second World War filled most of the gaps, and in the past two decades there has been a flood of data from Earth observation satellites. But modern atlases are still based on survey data obtained before the advent of satellite photography. Until now, cartographers have not used the combination of new mathematics and computing power needed to exploit this mass of data.
It has taken an outsider to change all this. The chaos theorist Mitchell Feigenbaum, who is professor of mathematics and physics at the Rockefeller University in New York, was brought in by the map publisher Hammond as an adviser on how best to computerise the production of a new atlas lie abandoned the conventional approach to computerised map making, which uses computers primarily to strip the labels off existing maps and add new ones. Instead, he set out to devise a complex program capable of producing the most accurate maps that could be made from the data available.
The publisher claims that the resulting atlas is the first to have been produced entirely from a computerised database which holds digitised information on billions of reference points from the latest satellite pictures of the Earth. Not only has the map labelling been computerised, so also has the redrawing of maps at different scales. The real revolution, though, lies in the continental maps. Drawn with levels of distortion lower than ever before, their mapping is based on an idea dating back to the early part of this century, now made practicable by computers and modern mathematics. Little of this is noticeable to the untrained eye, since much of what the computers have done automates the skills of the expert cartographer. "We wanted the computer to do absolutely as much as possible unassisted, but in no way violating the integrity of the aesthetics with which a human would have done it," says Feigenbaum.

Flattening the globe
Cartography is dogged by the problem of how to transfer distances on the curved surface of the Earth to the flat surface of a map. Methods for doing this are called projections, a term derived from geometric approaches that take points on the spherical Earth and project them onto another three- dimensional surface which can then be flattened into a map. Cylindrical projections, for example, represent lines of latitude as horizontal lines on a cylinder, and those of longitude as vertical lines. The cylinder is then cut along its length and unrolled to give a flat map.
The choice of projection depends partly on the purpose of the map and partly on the size of the area the cartographer wants to depict. No flat map can show accurately all three crucial attributes of the area being mapped: the distance between points, the area within a given boundary, and the shape of a given area. For atlases, where a broad representation of the Earth's surface is required rather than precision in any one attribute, the main inaccuracies are distortion of shape or distance. On large-scale maps the difference between curved distance and flat distance is negligible and can be ignored. But as the area being mapped grows, so does the potential for distortion -areas even a few tens of miles across must take account of the Earth's curvature. The cartographer has to decide where distortions will cause least damage, given the map's purpose. This is where the choice of projection is crucial.
Some projections aim to produce maps in which the angles, and therefore the shapes on the paper, are as close as possible to those on the ground. With these so-called conformal maps, the distortion occurs in the distances between points and in the areas within boundaries. The projection developed in 569 by Gerardus Mercator is a cylindrical conformal projection. It gives considerable distortion at high latitudes but has the advantage that compass bearings are consistent at all points on the map. Any path along a particular compass direction therefore appears as a straight line on a Mercator projection, which is why it is still the basis of most charts used for navigation. There is, however, no conformal way to show the entire surface of the Earth without infinitely distorting some areas.

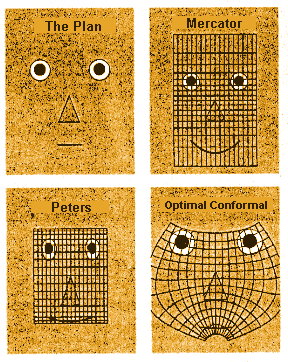Distorted world-view: the optimal conformal projection represents the plan more faithfully than either the Mercator or Peters projections

Other projections aim to show surface areas in correct proportion to each other. These "equal-area" maps, such as the Peters projection, became popular in the 1980s because of their attribute of depicting country sizes in true proportion- unlike the Mercator projection, which minimises the areas of most Third World countries, as they tend to be near the equator, and maximises areas near the poles. But the price of this is a huge distortion of shape.

Best of all possible worlds
On the basis that the best map is that with the least distortion of any sort, Feigenbaum asserts that the whole idea of equal area maps may be flawed. "It is very difficult to judge whether areas are equal," he argues. "The only things that human eyes can judge is linear distances."
Conformal projections have been used throughout the new Hammond atlas. Some are familiar, such as the Lambert conic conformal projection. This projects surface detail onto a truncated cone arranged to intersect with the Earth's surface along two circles of longitude that become the top and bottom of the map. The atlas uses the Lambert projection for the large-scale country maps, while the global maps have been made using the Robinson projection, a compromise between conformal and equal-shape maps that attempts to balance all the distortions. However, the continental maps are more revolutionary, since no single projection has been used.
They rely on the fact that for any chosen area on the surface of the Earth there is a projection which produces the best possible conformal map. Feigenbaum therefore designed a computer program that takes data about the boundary around an area to be mapped and calculates what the "optimal conformal projection" (the projection that minimises inaccuracies) will be. The map of South America, for example, is better than 98 per cent accurate; other atlases score around 95 per cent. Feigenbaum's maps of regular shapes such as Australia have a very small distortion, while Africa and North America may be distorted by 3 per cent. "These maps are uniformly twice as good as any projection that has ever been made before," says Feigenbaum.
The idea of the optimal conformal projection was first conjectured by the Russian mathematician Pafnutii Lvovich Tchebychev in the middle of the last century. However, it is only recent developments in computing that have allowed Tchebychev's theory to be put into practice.
In essence, the method is this: the relationship between a distance on the Earth's surface and a distance on the map is known as the scale factor. On a globe, the scale factor is constant throughout. This is not the case on a map because of the distortions caused when you flatten the curved surface: on any map the scale factor varies from point to point.
"You want to find that analytic function which produces a map for which the scale factor is as constant as possible," explains Feigenbaum. "The solution to that problem turns out to be that the scale factor must be constant on the boundary around the area you are mapping." Calculating this constant scale factor provides information that can be fed into a set formula. Solving this tells the computer how to manipulate data representing all the points within the map so that the distortion across the whole map is as small as possible.
The conformal projection selected by this method is, by definition, the best possible for the area in question. Careful selection of the area can reduce the distortion, but beyond that, the only improvement would be to show that some other system could perform better than conformal projection. "I'm sceptical that is possible," says Feigenbaum. "But I don't know how to prove that."
The labelling method designed by Feigenbaum uses a computer to tackle the problem, much in the way a human would. Previous computerisations have perversely chosen rule-based methods that restrict a label to a limited number of positions around the point it refers to. Feigenbaum treats the space around a point as a continuum, and takes into account the space available in the whole of the mapped area. The system is based on simple electrostatics: the labels are made to behave as though they are charged entities moving in a field which makes them appear to "flow" along parallels in the part of the world being mapped. Other rules maintain an acceptable association between point and label, and prevent overlap. "It's a molecular dynamical calculation. Every one of these things is busily buzzing around, seeking some decent equilibrium."

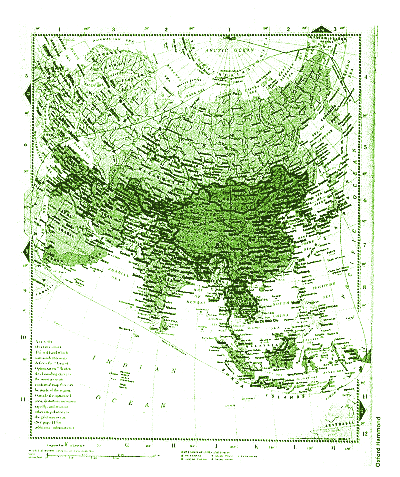Doing the continental: optical conformal maps in the new Hammond atlas are twice as accurate as other continental maps. The red line marks the boundary of the map, beyond which distortion occurs

The fractal factor
Another human skill automated for the new atlas comes into play when changing the scales. The data used to produce the maps is fractal: the closer you get to it the more structure emerges. This makes for problems when scaling a map up or down because it is not possible simply to magnify or reduce the existing boundaries. Going from a detailed large-scale map to a smaller scale, a smooth line of fractal data will turn into a highly irregular broad line. "A cartographer would see this more precise data and then, by his own training, figure out a much simpler curve to cast through it that would have the right integrity at that much smaller scale," explains Feigenbaum.
The computer does something similar. It examines the detailed fractal data and analyses the hierarchy to determine what the data represent and which points have greatest significance. On a small-scale map of the Scandinavian coast, for instance, it is not good enough simply to smooth over the smaller fiords. Any town at the head of one of these fiords would appear land-locked on the map. But if the computer program contains the instruction that any coastal town must appear as such on the smaller scale, it can draw a suitably sinuous line.
Only one part of the new atlas is not automated. The relief maps are produced by photographing handmade relief models. Relief data for the whole world are not good enough for automation, and no on is sure how best to treat the surface of the Earth mathematically. A mountain range is neither sufficiently smooth for conventional surface analysis, nor is it entirely fractal. "The whole geometry of these mountains is immensely interesting," says Feigenbaum. "At the moment we do not own any of the mathematics that allows us to understand surfaces for which the normal is varying in a more peculiar way-that perhaps have partial planes and then suddenly change."
Feigenbaum sees his next challenge as solving this remaining problem. This, together with further developments of the satellite database will mean maps could look very different in the 21st century. "There is the potential," says Feigenbaum, "to make archival, truly wonderful images of the Earth."

Author

Ian Mundell is a freelance journalist.