Is the Solar System stable?

Carl Murray

You might be surprised to learn that the Earth's orbit round the Sun, like those of other planets,is chaotic. What does this mean for the future of the Solar System?

People tend to think of the Solar System as a paradigm of order and regularity. We imagine the planets fixed in their orbits around the Sun for all time - an orderly, predictable, unchanging, majestic clockwork that never needs rewinding. We can steer the Voyager 2 spacecraft nearly 5 billion kilometres on a 12-year journey from the Earth to an encounter with Neptune, so it arrives on schedule within kilometres of its target. We can accept unforeseen changes in our everyday lives and even come to terms with natural and man-made disasters, yet we still have faith in the immutability of the orbits of the planets and satellites.

What grounds do we have for such beliefs? Is the behaviour of the Solar System completely predictable, or could the planets ever collide? This is a question that many astronomers have attempted to answer, but it is only in this decade that a better understanding of the problem and a possible  solution has emerged. The key to this progress is the study of chaos, even simple, deterministic equations can give complicated unpredictable solutions. Chaos has revealed that our Solar System is not the paragon of predictability that we once imagined.

In the 17th century Isaac Newton showed that if two bodies attract each other with force that was proportional to the square of the distance between them, then the resulting motion of body relative to the other would be a precise mathematical curve called a conic section (that is, a circle, ellipse, parabola or hyperbola). Although Newton was not the first person to suggest that the inverse square law of force was responsible for the motion of the planets, his great triumph was to provide a mathematical proof of the consequences of such a law.

He showed that a planet moving under the effects of the Sun' s gravity would describe an elliptical path, and that the period of this motion would depend only on the average distance from the Sun. In mathematical terms, he could show that the "two-body problem" was integrable, in other words, that it was possible to obtain a complete, practical solution to the problem using relatively simple mathematical equations. So, if we are interested only in the two-body problem we can predict any future configuration of the system with an arbitrary precision for all time.

But the Solar System is not composed of just two bodies. It is the Sun' s gravitational field dominates the motion of planets and that, to a good first approximation, each an elliptical orbit around the Sun. The planets also influence each other's motion, however, all according to the inverse square law. And we can detect these effects although they are small. For example, the basic ellipse of the Earth's orbit is not fixed in space:it gradually rotates or precesses, at a current rate of 0.3 degrees per century due to perturbations by the other planets,most notably Jupiter.

French mathematician Pierre Simon de Laplace tried to solve the problem of the Solar System's stability by making some simplifying assumptions about the nature of the gravitational interactions of the planets. Laplace showed that his simplified system was integrable and that  there were long-term periodicities (typically,tens of thousands of years) in the movement of the orbits of the planets: he thought he had achieved the elusive analytical solution. Unfortunately,the very terms that Laplace had neglected in his theory were those that could provide possible sources of chaos. So Laplace' s proof of stability has to be discounted.

Laplace was one of many scientists who had a fundamental  belief that once you had determined the laws governing the Universe, it was just a matter of solving the equations, with the appropriate starting conditions, to discover its past and future behaviour and that "nothing would be uncertain". The study of chaos has revealed that even completely deterministic systems, such as those involving gravitational interactions, can be chaotic and that Laplace's world-view was wrong. For example, the motion of the ball in a spinning roulette wheel is, in principle, a deterministic system. Although the ball and wheel are subject to known forces, trying to predict the final outcome is unlikely to be a rewarding experience.

We now know that, except for special cases, the general motion of many (n) bodies interacting through gravity, the "n-body problem", is not integrable. A simpler task is to attempt to solve the three-body problem. At the end of the 19th century, the French mathematician Henri Poincaré tackled this problem in some depth. It is clear from his writings that he was aware of the unpredictability of some solutions of the equations of motion. He did not solve the three-body problem; in fact, he proved that a simple, general solution did not exist. However, Poincaré was the first to appreciate the complicated behaviour that could result from the gravitational interaction of just three bodies. He also realised that in the Solar System, chaos and order, stability and instability were closely connected with a phenomenon called "resonance" (see "Asteroids and planets in resonance",below).

Resonance pervades the Solar System. It happens when any two periods have a simple numerical ratio. The most fundamental period for an object in the Solar System is its orbital period. This is the time it takes to complete one orbit and depends only on its distance from the central object. For example, the Jovian satellite Io has an orbital period of 1.769 days, nearly half that of the next satellite Europa - with a period 3.551 days. They are said to be in a 2: 1 orbit-orbit resonance. This particular resonance has important consequences because the perturbations, resulting from Europa' s gravity, force the orbit of Io to become more elongated,or eccentric. As Io moves closer to Jupiter and then further away in the course of a orbit, it experiences significant tidal stresses resulting in the active volcanoes that Voyager observed.

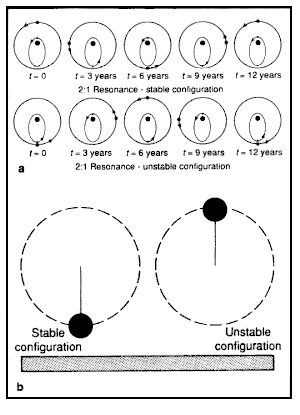A resonance may happen when there is a simple numerical relationship between two periods leads to repeated configurations. Consider the case of an asteroid and Jupiter orbiting the Sun. For simplicity, we will be take Jupiter's orbit to be circular and assume that all objects orbit in the same plane.An asteroid at the 2:1 Jovian resonance will have orbital period of six years,which is half Jupiter' s period of 12 years. To see how the resonance can be stable or unstable,consider two possible initial configurations with the asteroid and Jupiter aligned with the Sun on the same side of their orbits (conjunction). The asteroid's orbit will be considerably affected by Jupiter if conjunctions occur when the asteroid is at its furthermost point from the Sun (aphelion) is where the two orbits are closest. In the stable case,conjunctions occur at the asteroid's closest point to the Sun (perihelion). The asteroid reaches the danger point of aphelion after three and nine years,but in each case Jupiter is a different point in its orbit. Every 12 years, the initial configuration repeats itself and so the asteroid always avoids conjunctions at aphelion and is in a stable resonant orbit. In the unstable case, conjunctions always occur at the asteroid's aphelion, leading to a repeated, unstable configuration that cannot continue (see Figure a). There is a simple analogy with the motion of a pendulum (see Figure b).

It is stable when you start the bob in the vertically down position. Any small shifts of the bob will cause oscillations about the stable point. However, if you start the bob in the vertically up position, it can remain balanced there only for a short time before it becomes unstable. In fact, the equations of motion of an asteroid in resonance with Jupiter are very similar to those of a simple pendulum. To introduce chaos into the pendulum system we need only to oscillate the point of suspension in a regular fashion. The equivalent action in the Sun- Jupiter-asteroid system would be to make the eccentricity of Jupiter' s orbit nonzero.

To make things more complicated, Europa is simultaneously in a 2: l resonance with the next satellite Ganymede, the trio being involved in an intricate configuration which Laplace had studied.
 In the Saturnian system, resonant pairs of satellites include Mimas and Tethys, Enceladus and Dione, and Titan and Hyperion. Resonances are curiously absent from the Uranian satellite system, although there have been recent explanations that invoke the effects of chaos. Among the planets, Jupiter, with a period of ll.86 years, and Saturn, with a period of 29.46 years, are close to a 5:2 resonance, yet the only true orbit-orbit resonance between planets is a curious 3:2 resonance between Neptune and Pluto. C. J. Cohen and E. C. Hubbard at the U S Naval Weapons Laboratory discovered this in l965, not by observation, but by a "numerical integration" of the system. When the equations of motion of a system cannot be solved by mathematics, a possible alternative is to solve  them using a digital computer . Although such a numerical integration provides less insight than a mathematical  solution,it is one of the most powerful tools in modern dynamical astronomy.

The most likely reason that resonance is so common in satellite systems is due to the effects of tides. As a satellite raises a tide on a planet,there is an exchange of angular momentum between the bodies,resulting in a change in the orbit of the satellite and in the spin of the planet. Consequently, the orbits of the natural satellites today may bear little resemblance to their original ones;this is certainly true in the case of the Moon. As a satellite evolves, its orbital period changes and it may encounter a resonance with another satellite. In certain circumstances, the satellites become locked in a resonance and continue to evolve tidally, so maintaining the resonant configuration.The planets do raise tides on the Sun but these are not so important because of the greater relative distances involved. This may explain the lack of orbit-orbit resonances in the planetary system.

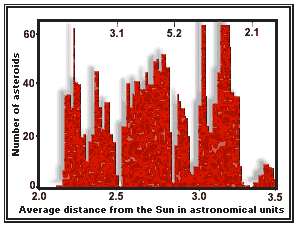Gaps in the asteroid belt occur at locations corresponding to resonances with Jupiter.

The most striking example of resonance occurs in the asteroid belt,a collection of more than 4000 catalogued objects orbiting between Mars and Jupiter. In l867, the American astronomer  Daniel Kirkwood noticed that the asteroid orbits were not randomly distributed. There were distinct gaps in the belt at locations that corresponded to resonances with Jupiter. For example,there were no asteroids at the 3:l resonance -  a distance  of 2.5 astronomical units - or at the 2: l resonance at 3-3 astronomical units (see the diagram above). This was the opposite situation to that found in the satellite systems where there was a preference for objects in resonance. Although there were fewer than 100 asteroids known in Kirkwood's day, his conclusions concerning the association with Jovian resonances were correct, but astronomers have only recently explained the gaps satisfactorily.

Astronomers had proposed several theories, ranging from the suggestion that the gaps were a kind of dynamical "illusion" , to the idea that increased collisions at the resonances had caused asteroid material to wear down, producing objects too small to be observed. In 1981, Stan Dermott and I began studies at Cornell University on how the asteroid orbits were distributed to try to find out which theory was correct. We concluded that you could explain the gaps in terms of a simple three-body problem involving the Sun, Jupiter and an asteroid. But we still lacked a mechanism that could actually remove an asteroid from a resonance, although we recognised that we could tackle the problem on a computer, by solving the equations of motion to study the behaviour of an asteroid over millions of years. The main drawback of such an approach was the expense - computer time is not cheap.

The breakthrough came in 1981 when Jack Wisdom, then a PhD student at the California Institute of Technology, developed a new numerical method for studying the motion of asteroids at resonance. Wisdom [Another pertinent name! -LB] knew about chaotic dynamics, and in particular how to derive "mappings" to speed up the numerical work. Given the state of a system at a certain time, a could give a precise, algebraic method for calculating the at some fixed time interval later. He still had to carry out the mapping on a computer, but using the mapping speeded up calculations 1000 times. As part of his thesis work, derived a mapping to study motion at the 3:1 Jovian resonance. He showed that asteroids, moving under the gravitational effects of the Sun and Jupiter, at this resonance could undergo large,unpredictable changes in their orbits. Such orbits were  chaotic.Wisdom  went on to show that these orbits crossed the orbit of Mars and would eventually impact or be scattered by the planets.

 This was the mechanism of removal that astronomers had been seeking. Wisdom showed that there was an extensive chaotic zone at the 3:1 resonance which matched the observed width of the gap. This discovery was to solve another problem in Solar System dynamics. Most people think that meteorites are fragments of asteroids that eventually collide with the Earth.You can measure the "age" of meteorites by finding out how long they have been  exposed to the cosmic rays in the Solar System. Members of one particular class of meteorite, the chondrites, have very short exposure ages of only a few million years.George Wetherill,of the Carnegie Institution in Washington DC, had shown that these meteorites had to come from the vicinity of the 3:1 resonance, but he lacked a mechanism. Wisdom provided the mechanism and carried out numerical integrations to show chaotic orbits of objects at the 3:1 resonances could  become eccentric enough for them to start crossing the Earth's orbit.

The whole problem of where objects in Earth-crossing orbits come from is more than an abstract academic question. The impact of a large asteroid on the Earth would be one of the worst natural disasters that our planet could face. The 3:1 gap is not entirely clear of asteroids. At least two asteroids in the gap, Alinda and Quetzalcoatl, are actually in resonance with Jupiter, and 1989 AC, the asteroid that will pass within just 0.011 astronomical units of the Earth in 2004, is also probably in resonance with Jupiter at the gap. It is important for dynamicists studying the Solar System to understand where such objects come from and how they evolve. This requires a knowledge of  chaos.

The two periods involved in a resonance relation do not have to be orbital periods. Another common form of resonance in the  Solar System is spin-orbit resonance, where the period of spin (the time it takes the orbit to rotate once about its axis) has a simple numerical relationship with its orbital period. For example,Mercury is locked in a 3:2 spin-orbit resonance.A more obvious example is our own Moon, which is in synchronous rotation because of the 1:1 spin-orbit resonance that forces it to keep the same face towards the Earth. The far side of the Moon was completely hidden from us until the era of spaceflight. Most natural satellites in the Solar System are in synchronous spin states although this was not their original state : they have evolved into such configurations because of tidal effects. A simple theory allows us to predict the timescales for evolution into the synchronous state. The timescale depends on the mass of the satellite and its distance from the central object.

Prior to the Voyager encounters with Saturn, people had wondered whether or not the satellite Hyperion was in synchronous rotation. After all, it is small and one of the most distant of the Saturnian satellites. Observations from Voyager 2 revealed an irregularly shaped object shaped rather like a hamburger, or a potato. Measurements of Hyperion's rotation made by Voyagers 1 and 2 suggest a spin period of 13 days, compared with an orbital period of 21 days, so Hyperion does not appear to be in an obvious spin-orbit resonance.

In 1984, Jack Wisdom and Stan Peale working at the University of California, Santa Barbara, and Francois Mignard of C E R G A, Grasse, published a classic paper in which they showed that the simple theory worked out for satellite rotations does not apply to Hyperion, because it is distinctly nonspherical. Hyperion's rotation is certainly not synchronous, but neither is it regular; it is chaotic. Furthermore, Wisdom, Peale and Mignard showed that Hyperion is also "attitude unstable" , which means that its spin axis is not fixed and the satellite is tumbling in space as well as rotating chaotically. In normal circumstances, the satellite orbit would become more circular and eventually the chaotic behaviour would disappear, but, ironically, tiny Hyperion is locked in an apparently stable 4:3 orbit-orbit resonance with the massive satellite of Saturn, Titan. This forces Hyperion's orbit to be eccentric rather than circular, so the chaos persists, resulting in a satellite with a chaotic spin but a regular orbit.

So chaotic motion does exist in the Solar System in a variety of forms. But are the orbits of the  planets chaotic? The answer to this question is likely to come from long-term integrations of the planetary system using a new generation of digital computers. In this decade, there have been a number of separate efforts to investigate the motions of Jupiter, Saturn, Uranus, Neptune and Pluto. The inner planets are notoriously difficult to include in such integrations because very small time-steps are needed to follow them accurately.

The Digital Orrery numerically integrates orbits in the Solar  System. It is attached to a computer workstation at the Massachusetts Institute of Technology and can study the motions of 10 gravitationally interacting bodies at 60 times the speed of a VAX minicomputer.

An international consortium of Solar System dynamicists led by Archie Roy of the University of Glasgow, carried out Project  LONGSTEP (Long-term Gravitational Study of the Outer Planets) on the Cray supercomputer at the University of London. This involved integrating the orbits of the outer planets for 100 years. Its results revealed several curious exchanges of energy between the outer planets, but no signs of gross instability . Another project involved constructing the Digital Orrery by  Gerry Sussman and his group from the Massachusetts Institute of Technology. The group used this machine, which has a computer architecture designed to mimic the interactions between the planets, to integrate the orbits of the outer planets over 845 million years (some 20 per cent of the age of the Solar System). In 1988, Sussman and Wisdom produced integrations using the Orrery which revealed that Pluto's orbit shows the tell-tale signs of chaos, due in part to its peculiar resonance with Neptune. This does not mean, however, that the resonance is unstable or that Pluto and Neptune could ever collide, even though their orbits intersect. Recent work suggests that this chaos arises from resonances within resonances; these can limit the extent of Pluto's wandering and preserve the main resonance with Neptune.

If  Pluto's orbit is chaotic, then technically the whole Solar System is chaotic, because each planet, even one as small as Pluto, affects the others to some extent through gravitational interactions. But we now realise that although chaos means that some orbits are unpredictable, it does not necessarily mean that planets will collide - chaotic motion can still be bounded. In 1989, Jacques Laskar of the Bureau des Longitudes in Paris published the results of his numerical integration of the Solar System over 200 million years. These were not the full equations of motion, but rather averaged equations along the lines of those used by Laplace. Unlike Laplace, however, Laskar's equations had some 150,000 terms. Laskar's work showed that the Earth's orbit (as well as the orbits of all the inner planets) is chaotic and that an error as small as 15 metres in measuring the position of the Earth today would make it impossible to predict where the Earth would be in its orbit in just over 100 million years' time.

Laskar's results still have to be confirmed by integrating the full equations of motion, but this will have to wait until the next generation of supercomputers arrives. Meanwhile, we can take comfort from the fact that his work does not imply that orbital catastrophe awaits our planet, only that its future path is unpredictable. It seems likely that the Solar System is chaotic but nevertheless confined, although we have yet to prove it.More than 300 years after the publication of Newton's Principia, we are still struggling to understand the full implications of his square law of gravity. We have begun to view our system of chaos in a light that is revealing the true intricacies of its majestic clockwork.

MAIN INDEX
REFERENCE GUIDE			TRANSCRIPTS				GLOSSARY
Chaos	Quantum	Logic	Cosmos	Conscious	Belief	Elect.	Art	Chem.	Maths

The New Scientist Guide to Chaos File Info: Created Updated 14/7/2002 Page Address: http://members.fortunecity.com/templarser/solarsys.html