The Power of One
Everyday numbers obey a law so unexpected it is hard to believe it's true.
Armed with this knowledge, it's easy to catch those who have been faking
research results or cooking the books.
Robert Matthews
|
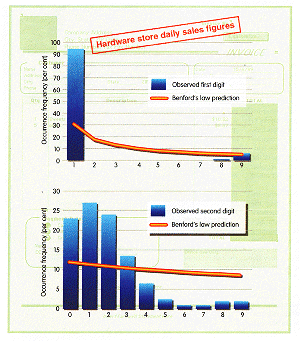
Alex had no idea what dark little secret he was about to uncover
when he asked his brother-in-law to help him out with his term project. As
an accountancy student at Saint Mary's University in Halifax, Nova Scotia,
Alex [not the student's real name] needed some real-life commercial figures
to work on, and his brother-in-law's hardware store seemed the obvious place
to get them.
Trawling through the year's sales figures, Alex could find nothing obviously
strange about them. Still, he did what he was supposed to do for his project,
and performed a bizarre little ritual requested by his accountancy professor,
Mark Nigrini. He went through the sales figures and made a note of how many
started with the digit 1. It came out at 93 per cent. He handed it in and
thought no more about it.
Later, when Nigrini was marking the coursework, he took one look at that
figure and realised that an embarrassing situation was looming. His suspicions
hardened as he looked through the rest of Alex's analysis of his brother-in-law's
accounts. None of the sales figures began with the digits 2 through to 7,
and there were just 4 beginning with the digit 8, and 21 with 9. After a
few more checks, Nigrini was in no doubt: Alex's brother-in-law was a fraudster,
systematically cooking the books to avoid the attentions of bank managers
and tax inspectors.
It was a nice try. At first glance, the sales figures showed nothing very
suspicious, with none of the sudden leaps or dives that often attract the
attentions of the authorities. But that was just it: they were too regular.
And this is why they fell foul of that ritual he had asked Alex to perform.
Because what Nigrini knew--and Alex's brother-in-law clearly didn't--was
that the digits making up the shop's sales figures should have followed a
mathematical rule discovered accidentally over 100 years ago. Known as Benford's
law, it is a rule obeyed by a stunning variety of phenomena, from
stock market prices to census data to the heat
capacities of chemicals. Even a ragbag of figures extracted from newspapers
will obey the law's demands that around 30 per cent of the numbers will start
with a 1, 18 per cent with a 2, right down to just 4.6 per cent starting
with a 9.
It is a law so unexpected that at first many people simply refuse to believe
it can be true. Indeed, only in the past few years has a really solid
mathematical explanation of its existence emerged. But after years of being
regarded as a mathematical curiosity, Benford's law is now being eyed by
everyone from tax inspectors to computer designers--all of whom think it
could help them solve some tricky problems with astonishing ease. In two
weeks' time, the US Institute of Internal Auditors will begin holding training
courses on how to apply Benford's law in fraud investigations, hailing it
as the biggest advance in the field for years.
The story behind the law's discovery is every bit as weird as the law itself.
In 1881, the American astronomer Simon Newcomb penned a note to the American
Journal of Mathematics about a strange quirk he'd noticed about books
of logarithms, then widely used by scientists performing calculations. The
first pages of such books seemed to get grubby much faster than the last
ones.
The obvious explanation was perplexing. For some reason, people did more
calculations involving numbers starting with 1 than 8 and 9. Newcomb came
up with a little formula that matched the pattern of use pretty well: nature
seems to have a penchant for arranging numbers so that the proportion beginning
with the digit D is equal to log10 of 1 + (1/D) (see
"Here, there and everywhere").
With no very convincing argument for why the formula should work, Newcomb's
paper failed to arouse any interest, and the Grubby Pages Effect was forgotten
for over half a century. But in 1938, a physicist with the General Electric
Company in the US, Frank Benford, rediscovered the effect and came up with
the same law as Newcomb. But Benford went much further. Using more than 20
000 numbers culled from everything from listings of the drainage areas of
rivers to numbers appearing in old magazine articles, Benford showed that
they all followed the same basic law: around 30 per cent began with the digit
1, 18 per cent with 2 and so on.
Like Newcomb, Benford did not have any really good explanation for the existence
of the law. Even so, the sheer wealth of evidence he provided to demonstrate
its reality and ubiquity has led to his name being linked with the law ever
since.
It was nearly a quarter of a century before anyone came up with a plausible
answer to the central question: why on earth should the law apply to so many
different sources of numbers? The first big step came in 1961 with some neat
lateral thinking by Roger Pinkham, a mathematician then at Rutgers University
in New Brunswick, New Jersey. Just suppose, said Pinkham, there really is
a universal law governing the digits of numbers that describe natural phenomena
such as the drainage areas of rivers and the properties of chemicals. Then
any such law must work regardless of what units are used. Even the inhabitants
of the Planet Zob, who measure area in grondekis, must find exactly the same
distribution of digits in drainage areas as we do, using hectares. But how
is this possible, if there are 87.331 hectares to the grondeki?
The answer, said Pinkham, lies in ensuring that the distribution of digits
is unaffected by changes of units. Suppose you know the drainage area in
hectares for a million different rivers. Translating each of these values
into grondekis will change the individual numbers, certainly. But overall,
the distribution of numbers would still have the same pattern as before.
This is a property known as "scale invariance".
Pinkham showed mathematically that Benford's law is indeed scale-invariant.
Crucially, however, he also showed that Benford's law is the only way to
distribute digits that has this property. In other words, any "law" of digit
frequency with pretensions of universality has no choice but to be Benford's
law.
Pinkham's work gave a major boost to the credibility of the law, and prompted
others to start taking it seriously and thinking up possible applications.
But a key question remained: just what kinds of numbers could be expected
to follow Benford's law? Two rules of thumb quickly emerged. For a start,
the sample of numbers should be big enough to give the predicted proportions
a chance to assert themselves. Second, the numbers should be free of artificial
limits, and allowed to take pretty much any value they please. It is clearly
pointless expecting, say, the prices of 10 different types of beer to conform
to Benford's law. Not only is the sample too small, but--more importantly--the
prices are forced to stay within a fixed, narrow range by market forces.
Random numbers
On the other hand, truly random numbers won't conform to Benford's law either:
the proportions of leading digits in such numbers are, by definition, equal.
Benford's Law applies to numbers occupying the "middle ground" between the
rigidly constrained and the utterly unfettered.
Precisely what this means remained a mystery until just three years ago,
when mathematician Theodore Hill of Georgia Institute of Technology in Atlanta
uncovered what appears to be the true origin of Benford's law. It comes,
he realised, from the various ways that different kinds of measurements tend
to spread themselves. Ultimately, everything we can measure in the Universe
is the outcome of some process or other: the random jolts of atoms, say,
or the exigencies of genetics. Mathematicians have long known that the spread
of values for each of these follows some basic mathematical rule. The heights
of bank managers, say, follow the bell-shaped Gaussian curve, daily temperatures
rise and fall in a wave-like pattern, while the strength and frequency of
earthquakes are linked by a logarithmic law.
Now imagine grabbing random handfuls of data from a hotchpotch of such
distributions. Hill proved that as you grab ever more of such numbers, the
digits of these numbers will conform ever closer to a single, very specific
law. This law is a kind of ultimate distribution, the "Distribution of
Distributions". And he showed that its mathematical form is...Benford's Law.
Hill's theorem, published in 1996, seems finally to explain the astonishing
ubiquity of Benford's law. For while numbers describing some phenomena are
under the control of a single distribution such as the bell curve, many
more--describing everything from census data to stock market prices--are
dictated by a random mix of all kinds of distributions. If Hill's theorem
is correct, this means that the digits of these data should follow Benford's
law. And, as Benford's own monumental study and many others have showed,
they really do.
Mark Nigrini, Alex's former project supervisor and now a professor of accountancy
at the Southern Methodist University, Dallas, sees Hill's theorem as a crucial
breakthrough: "It . . . helps explain why the significant-digit phenomenon
appears in so many contexts."
It has also helped Nigrini to convince others that Benford's law is much
more than just a bit of mathematical frivolity. Over the past few years,
Nigrini has become the driving force behind a far from frivolous use of the
law: fraud detection.
In a ground-breaking doctoral thesis published in 1992, Nigrini showed that
many key features of accounts, from sales figures to expenses claims, follow
Benford's law--and that deviations from the law can be quickly detected using
standard statistical tests. Nigrini calls the fraud-busting technique "digital
analysis", and its successes are starting to attract interest in the corporate
world and beyond.
Some of the earliest cases--including the sharp practices of Alex's store-keeping
brother-in-law--emerged from student projects set up by Nigrini. But soon
he was using digital analysis to unmask much bigger frauds. One recent case
involved an American leisure and travel company with a nationwide chain of
motels. Using digital analysis, the company's audit director discovered something
odd about the claims being made by the supervisor of the company's healthcare
department. "The first two digits of the healthcare payments were checked
for conformity to Benford's law, and this revealed a spike in numbers beginning
with the digits '65'," says Nigrini. "An audit showed 13 fraudulent cheques
for between $6500 and $6599...related to fraudulent heart surgery claims
processed by the supervisor, with the cheque ending up in her hands."
Benford's law had caught the supervisor out, despite her best efforts to
make the claims look plausible. "She carefully chose to make claims for employees
at motels with a higher than normal number of older employees," says Nigrini.
"The analysis also uncovered other fraudulent claims worth around $1 million
in total."
Not surprisingly, big businesses and central governments are now also starting
to take Benford's law seriously. "Digital analysis is being used by listed
companies, large private companies, professional firms and government agencies
in the US and Europe--and by one of the world's biggest audit firms," says
Nigrini.
Warning signs
The technique is also attracting interest from those hunting for other kinds
of fraud. At the International Institute for Drug Development in Brussels,
Mark Buyse and his colleagues believe Benford's law could reveal suspicious
data in clinical trials, while a number of university researchers have contacted
Nigrini to find out if digital analysis could help reveal fraud in laboratory
notebooks.
Inevitably, the increasing use of digital analysis will lead to greater awareness
of its power by fraudsters. But according to Nigrini, that knowledge won't
do them much good--apart from warning them off: "The problem for fraudsters
is that they have no idea what the whole picture looks like until all the
data are in," says Nigrini. "Frauds usually involve just a part of a data
set, but the fraudsters don't know how that set will be analysed: by quarter,
say, or department, or by region. Ensuring the fraud always complies with
Benford's Law is going to be tough--and most fraudsters aren't rocket
scientists."
In any case, says Nigrini, there is more to Benford's law than tracking down
fraudsters. Take the data explosion that threatens to overwhelm computer
data storage technology. Mathematician Peter Schatte at the Bergakademie
Technical University, Freiberg, has come up with rules that optimise computer
data storage, by allocating disk space according to the proportions dictated
by Benford's law.
Ted Hill at Georgia Tech thinks that the ubiquity of Benford's law could
also prove useful to those such as Treasury forecasters and demographers
who need a simple "reality check" for their mathematical models. "Nigrini
showed recently that the populations of the 3000-plus counties in the US
are very close to Benford's law," says Hill. "That suggests it could be a
test for models which predict future populations--if the figures predicted
are not close to Benford, then rethink the model."
Both Nigrini and Hill stress that Benford's law is not a panacea for
fraud-busters or the world's data-crunching ills. Deviations from the law's
predictions can be caused by nothing more nefarious than people rounding
numbers up or down, for example. And both accept that there is plenty of
scope for making a hash of applying it to real-life situations: "Every
mathematical theorem or statistical test can be misused--that does not worry
me," says Hill.
But they share a sense that there are some really clever uses of Benford's
law still waiting to be dreamt up. Says Hill: "For me the law is a prime
example of a mathematical idea which is a surprise to everyone--even the
experts."
