The Challenge of Large Numbers

As computer capabilities increase, mathematicians can better characterize and manipulate gargantuan figures. Even so, some numbers can only be imagined

Richard E. Crandall

Large numbers have a distinct appeal,a majesty if you will. In a sense that they lie at the limits of the human imagination which is why they have long proved elusive,difficult to define,and harder still to manipulate. In recent decades though computer capabilities have dramatically improved. Modern machines now possess enough memory and speed to handle quite impressive figures.For instance it is possible to multiply together million-digit numbers in a mere fraction of a second. As a result we can now characterize numbers about which earlier mathematicians could only dream.
Interest in large numbers dates back to ancient times. We know, for example that the early Hindus, who developed the decimal system, contemplated them .In the now commonplace decimal system the position of a digit (1s, 10s, 100s and so on) denotes its scale. Using this shorthand, the Hindus named many large numbers; one having 153 digits or as we might say today, a number of of the order 10¹⁵³-is mentioned in a myth about Buddha.
The ancient Egyptians, Romans and Greeks pondered large values as well. But historically, a large number was whatever the prevailing culture deemed it to be an intrinsically circular definition. The Romans initially had no terms or symbols for figures above 100,000. And the Greeks usually stopped counting at a myriad ,word meaning "10,000." Indeed, a popular idea in ancient Greece was that no number was greater than the total count of sand grains needed to fill the universe.
In the third century B.C., Greek mathematician Archimedes sought to correct this belief. In a letter to King Gelon of Syracuse, he set out to calculate the actual number of sand grains in the universe. To do so, Archimedes devised a clever scheme involving successive ratios that would effectively extend the prevailing Greek number system, which had no exponential scaling. His results, which in current terms placed the number somewhere between 10⁵¹ to 10⁶³ were visionary; in fact, a sphere having the radius of Pluto's orbit would contain on the order of 10⁵¹ grains.
Scholars in the 18th and 19th centuries contemplated large numbers that still have practical scientific relevance. Consider Avogadro's number; named after the 19th-century Italian chemist Amedeo Avogadro. It is roughly 6.02 x 10²³ and represents the number of atoms in 12 grams of pure carbon. One way to think about Avogadro's number, also called a mole, is as follows: if just one gram of carbon were expanded to the size of planet Earth, a single carbon atom would loom something like a bowling ball.
Another interesting way to imagine a mole is to consider the total number of computer operations-that is, the arithmetic operations occurring within a computer's circuits - ever performed by all computers in history. Even a small machine can execute millions of operations per second; mainframes can do many more. Thus, the total operation count to date, though impossible to estimate precisely, must be close to a mole. It will undoubtedly have exceeded that by the year 2000.
Today scientists deal with numbers much larger than the mole. The number of protons in the known universe, for example, is thought to be about 10⁸⁰. But the human imagination can press further. It is legendary that the nine-year-old nephew of mathematician Edward Kasner did coin, in 1938, the googol, as 1 followed by 100 zeroes, or 10¹⁰⁰. With respect to some classes of computational problems, the googol roughly demarcates the number magnitudes that begin seriously to challenge modern machinery. Even so, machines can even answer some questions about gargantuan as large as the mighty googolplex, which is 1 followed by a googol of zeroes, or ₁₀10¹⁰⁰. Even if you used a proton for every zero, you could not scribe the googolplex onto the known universe.

WAV 257K

Manipulating the Merely Large
Somewhat above the googol lie numbers that present a sharp challenge to practitioners of the art of factoring: the art of breaking numbers into their prime factors, where primes are themselves divisible only by 1 and themselves. For example, 1,799,257 factors into 7,001 x 257, but to decompose a sufficiently large number into its prime factors can be so problematic that computer scientists have harnessed this difficulty to encrypt data. Indeed, one prevailing encryption algorithm, called RSA, transforms the problem of cracking encrypted messages into that of factoring certain large numbers, called public keys. (RSA is named after its inventors, Ronald L. Rivest of the Massachusetts Institute of Technology, Adi Shamir of the Weizmann Institute of Science in Israel and Leonard M. Adleman of the University of Southern California.
To demonstrate the strength of RSA, Rivest,Shamir and Adleman challenged readers of Martin Gardner's column in the August 1977 issue of Scientific American to factor a 129-digit number, dubbed RSA-129, and find a hidden message. It was not until 1994 that Arjen K. Lenstra of Beilcore, Paul Leyland of the University of Oxford and then graduate student Derek Atkins of M.I.T and undergraduate student Michael Graff of Iowa State University, working; with hundreds of colleagues on the Internet, succeeded. (The secret encrypted message was "THE MAGIC WORDS ARE SQUEAMISH OSSIFRAGE.") Current recommendations suggest that RSA encryption keys have at least 230 digits to be secure.
Network collaborations are now common place, and a solid factoring culture has sprung up. Samuel S. Wagstaff, Jr., of Purdue University maintains a factoring newsletter listing recent factorizations. And along similar lines, Chris K. Caldwell of the University of Tennessee at Martin maintains a World Wide Web site (http://www.utm.edu/research/primes/largest.html) for prime number records. Those who practice factoring typically turn to three powerful algorithms. The Quadratic Sieve (QS) method, pioneered by Carl Pomerance of the University of Georgia in the 1980s, remains a strong, general-purpose attack for, factoring numbers somewhat larger than a googol. (The QS,in fact, conquered RSA-129.) To factor a mystery number,the QS attempts to factor many smaller, related numbers,generated via a clever sieving process. These smaller factorizations are combined to yield a factor of the mystery number .

LARGE NUMBERS- such as the 100-digit, or googol-size, ones running across the tops of these pages - have become more accessible over time thanks to advances in computing. Archimedes, whose bust appears at the left, had to invent new mathematics to estimate the number of sand grains required to fill the universe. His astonishingly accurate result, 1051, was by ancient standards truly immense. Modern machines, however, routinely handle vastly greater values. Indeed, any personal computer with the right software can completely factor a number of order 1051.

A newer strategy, the Number Field Sieve (NFS), toppled a 155 - digit number,the ninth Fermat number, F₉ (Named for the great French theorist Pierre de Fermat, the nth Fermat number is F_n= ₂2ⁿ + 1.) In 1990 F₉ fell to Arien Lenstra, Hendrik W Lenstra, Jr., of the University of California at Berkeley, Mark Manasse of Digital Equipment Corporation and British mathematician John Pollard, again aided by a substantial machine network. This spectacular factorization depended on F₉'s special form. But Joseph Buhler of Reed College, Hendrik Lenstra and Pomerance have since developed a variation of the NFS for factoring arbitrary numbers. This general NFS can, today, comfortably factor numbers of 130 digits. In retrospect, RSA-129 could have been factored in less time this way.
The third common factoring tactic, the Elliptic Curve Method (ECM), developed by Hendrik Lenstra, can take apart much larger numbers, provided that at least one of the number's prime factors is sufficiently small. For example, Richard P. Brent of the Australian National University recently factored F₁₀ using ECM, after first finding a single prime factor "only" 40 digits long. It is difficult to find factors having more than 40 digits using ECM. For arbitrary numbers between, say,10¹⁵⁰ and 10^1,000,000, ECM stands as the method of choice, although ECM cannot be expected to find all factors of such gargantuan numbers.
Even for numbers that truly dwarf the googol, isolated factors can sometimes be found using a centuries-old sieving method. The idea is to use what is called modular arithmetic, which keeps the sizes of numbers under control so that machine memory is not exceeded, and adroitly scan ("sieve") over trial factors. A decade ago Wufrid Keller of the University of Hamburg used a sieving technique to find a factor for the awesome F₂₃₄₇₁, which has roughly 10^7,000 decimal digits. Keller's factor itself has "only" about 7,000 digits. And Robert J. Harley, then at the California Institute of Technology, turned to sieving to find a 36-digit factor for the stultifying (googolplex + 1); the factor is 316,912,650, 057,057,350,374,175,801 ,344,000,001.

Algorithmic Advancements
Many modern results on large numbers have depended on algorithms from seemingly unrelated fields. One example that could fairly be called the workhorse of all engineering algorithms is the Fast Fourier Transform (FFT). The FFT is most often thought of as a means for ascertaining some spectrum as is done in analyzing birdsongs or human voices or in properly tuning an acoustic auditorium. It turns out that ordinary multiplication,a fundamental operation between numbers-can be dramatically enhanced via FFT [see box below]. Arnold Schonage of the University of Bonn and others refined this astute observation into a rigorous theory during the 1970s.
FFT multiplication has been used in celebrated calculations of p to a great many digits. Granted p is not a bona fide large number; but to compute p to millions of digits involves the same kind of arithmetic used in large-number studies. In 1985 R. William Gosper, Jr., of Symbolics, Inc., in Palo Alto, Calif., computed 17 million digits of it. A year later David Bailey of the National Aeronautics and Space Administration Ames Research Center computed p to more than 29 million digits. More recently, Bailey and Gregory Chudnovsky of Columbia University reached one billion digits.

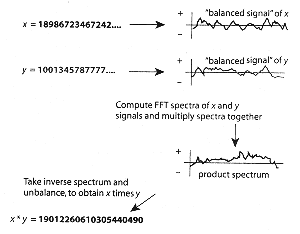
Using Fast Fourier Transforms for Speedy Multiplication
Ordinary multiplication is a long-winded process by any account, even for relatively small numbers: To multiply two numbers, x and y, each having D digits, the usual, "grammar school" method involves multiplying each successive digit of x by every digit of y and then adding columnwise, for a total of roughly D2 operations. During the 1970s, mathematicians developed means for hastening multiplication of two D-digit numbers by way of the Fast Fourier Transform (FFT). The FFT reduces the number of operations down to the order of D log D. (For example, for two 1,000-digit numbers, the grammar school method may take more than 1,000,000 operations, whereas an FFT might take only 50,000 operations.) A full discussion of the FFT algorithm for multiplication is beyond the scope of this article.In brief, the digits of two numbers, x and y (actually, the digits in some number base most convenient for the computing machinery) are thought of as signals. The FFT is applied to each signal in order to decompose the signal into its spectral components.	This is done in the same way that a biologist might decompose a whale song or some other meaningful signal into frequency bands. These spectra are quickly multiplied together, frequency by frequency.Then an inverse FFT and some final manipulations are performed to yield the digits of the product of x and y. There are various, powerful modern enhancements to this basic FFT multiplication. One such enhancement is to treat the dig it signals as bipolar, meaning both positive and negative digits are allowed. Another is to "weight" the signals by first multiplying each one by some other special signal. These enhancements have enabled mathematicians to discover new prime numbers and prove that certain numbers are prime or composite (not prime). - R.E.C.

And Yasumasa Kanada of the University of Tokyo has reported five billion digits. In case anyone wants to check this at home, the one-billionth decimal place of p , Kanada says, is nine.
FFT has also been used to find large prime numbers. Over the past decade or so, David Slowinski of Cray Research has made a veritable art of discovering record primes. Slowinski and his co- worker Paul Gage uncovered the prime 2^1,257,787 - 1 in mid-1996. A few months later, in November; programmers Joel Armengaud of Paris and George F Woltman of Orlando, Fla., working as part of a network project run by Woltman, found an even larger prime: 2^1,398,269 - 1. This number; which has over 400,000 decimal digits, is the largest known prime number as of this writing. It is, like most other record holders, a so-called Mersenne prime. These numbers take the form 2^q - 1, where q is an integer, and are named after the 17th- century French mathematician Marin Mersenne.
For this latest discovery, Woltman optimized an algorithm called an irrational-base discrete weighted transform, the theory of which I developed in 1991 with Barry Fagin of Dartmouth College and Joshua Doenias of NeXT Software in Redwood City, Calif. This method was actually a by-product of cryptography research at NeXT.
Blaine Garst, Doug Mitchell, Avadis Tevanian, Jr., and I implemented at NeXT what is one of the strongest-if not the strongest encryption schemes available today, based on Mersenne primes. This patented scheme, termed Fast Elliptic Encryption (FEE), uses the algebra of elliptic curves, and it is very fast. Using, for example, the newfound Armengaud-Woltman prime 2^1,398,269 - 1 as a basis, the FEE system could readily encrypt this issue of Scientific American into seeming gibberish. Under current number- theoretical beliefs about the difficulty of cracking FEE codes, it would require, without knowing the secret key, all the computing power on earth more than 10^10,000 years to decrypt the gibberish back into a meaningful magazine.
Just as with factoring problems, proving that a large number is prime is much more complicated if the number is arbitrary-that is, if it is not of some special form, as are the Mersenne primes. For primes of certain special forms, "large" falls somewhere in the range of 2^1,000,000. But currently it takes considerable computational effort to prove that a "random" prime having only a few thousand digits is indeed prime. For example, in 1992 it took several weeks for Francois Morian of the University of Claude Bernard, using techniques developed jointly with A.O.L. Atkin of the University of Illinois, and others, to prove by computer that a particular 1,505-digit number, termed a partition number, is prime.

Colossal Composites
It is quite a hit easier to prove that some number is not prime (that it is composite, that is, made up of more than one prime factor). In 1992 Doenias, Christopher Norrie of Amdahl Corporation and I succeeded in proving by machine that the 22nd Fermat number, ₂2²² + 1, is composite. This number has more than one million decimal digits. Almost all the work to resolve the character of F₂₂ depended on yet another modification of FFT multiplication. This proof has been called the longest calculation ever performed for a "one-bit," or yes-no, answer; and it took about 10¹⁶ computer operations. That is roughly the same amount that went into generating the revolutionary Pixar-Disney movie Toy Story, with its gloriously rendered surfaces and animations.

COLOSSI become somewhat easier to contemplate-and compare-if one adopts a statistical view. For instance, it would take approximately 103,000,000 years before a parrot, pecking randomly at a keyboard, could reproduce by chance The Hound of the Baskervilles. This time span, though enormous, pales in comparison to the 101033 years that would elapse before fundamental quantum fluctuations might topple a beer can on a level surface.

Although it is natural to suspect the validity of any machine proof, there is a happy circumstance connected with this one. An independent team of Vilmar Trevisan and Joao B. Carvaiho, working at the Brazilian Supercomputer Center with different machinery and software (they used, in fact, Bailey's FFT software) and unaware of our completed proof, also concluded that F₂₂ is composite. Thus, it seems fair to say, without doubt, that F₂₂ is composite. Moreover F₂₂ is also now the largest "genuine" composite known-which means that even though we do not know a single explicit factor for F₂₂ other than itself and 1, we do know that it is not prime.
Just as with Archimedes' sand grains in his time, there will always be colossal numbers that transcend the prevailing tools. Nevertheless, these numbers can still be imagined and studied. In particular; it is often helpful to envision statistical or biological scenarios. For instance, the number 10 to the three-millionth power begins to make some intuitive sense if we ask how long it would take a laboratory parrot, pecking randomly and tirelessly at a keyboard, with a talon occasionally pumping the shift key, say, to render by accident that great detective epic, by Sir Arthur Conan Doyle, The Hound of the Baskervilles. To witness a perfectly spelled manuscript, one would expect to watch the bird work for approximately 10^3,000,000 years. The probable age of the universe is more like a paltry 10¹⁰ years.

How large is large?

To get a better sense of how enormous some numbers truly are,imagine that the 10-digit number representing the age in years of the visible universe were a single word on a page. Then the number of protons in the visible universe, about 1080, would look like a sentence. The ninth Fermat number - which has the value Fn=22n+1 (where n is nine) - would take up several lines. The tenth Fermat number would look something like a paragraph of digits. A thousand digit number, pressing the upper limit for primality testing, would look like a page of digits. The largest known prime number,21,398,269-1 in decimal form,would essentially fill an issue of Scientific American. A book could hold all the digits of the 22nd Fermat number, which possesses more than one million digits and is now known to be composite To multiply together two "bookshelves" even on a scalar supercomputer, takes about one minute. 101033 written in decimal form would fill a library much larger than the earth's volume.In fact, there are theoretically important numbers that cannot be written down in this universe,even using exponential notation.

But 10^3,000,000 is as nothing compared with the time needed in other scenarios. Imagine a full beer can, sitting on a level, steady, rough-surfaced table, suddenly toppling over on its side, an event made possible by fundamental quantum fluctuations. Indeed, a physicist might grant that the quantum wave function of the can does extend, ever so slightly, away from the can so that toppling is not impossible. Calculations show that one would expect to wait about ₁₀10³³ years for the surprise event. Unlikely as the can toppling might be, one can imagine more staggering odds. What is the probability, for example, that sometime in your life you will suddenly find yourself standing on planet Mars, reassembled and at least momentarily alive? Making sweeping assumptions about the reassembly of living matter, I estimate the odds against this bizarre event to be ₁₀10⁵¹ to 1. To write these odds in decimal form, you would need a 1 followed by a zero for every one of Archimedes' sand grains. To illustrate how unlikely Mars teleportation is, consider that the great University of Cambridge mathematician John Littlewood once estimated the odds against a mouse living on the surface of the sun for a week to be ₁₀10⁴² to 1.
These doubly exponentiated numbers pale in comparison to, say, Skewes's number, 10^ (₁₀10³⁴), which has actually been used in developing a theory about the distribution of prime numbers. To show the existence of certain difficult-to-compute functions, mathematicians have invoked the Ackermann numbers (named after Wilhelm Ackermann of the Gymnasien in Luedenscheid, Germany), which compose a rapidly growing sequence that runs: 0, 1, 2², 3^ ( ₃3³)..... The fourth Ackermann number, involving exponentiated 3's, is approximately 10^{3,638,334,640,024}. The fifth one is so large that it could not be written on a universe-size sheet of paper, even using exponential notation! Compared with the fifth Ackermann number, the mighty googolplex is but a spit in the proverbial bucket.

The Author

RICHARD E. CRANDALL is chief scientist at NeXT Software. He is also Vollum Adjunct Professor of Science and director of the Center for Advanced Computation at Reed College. Crandall is the author of seven patents, on subjects ranging from electronics to the Fast Elliptic Encryption system. In 1973 he received his Ph.D. in physics from the Massachusetts Institute of Technology.

Further Reading

THE WORKS OF ARCHIMEDES. Edited by T. L. Heath. Cambridge University Press, 1897.
THE WORLD OF MATHEMATICS. Edward Kasner and James R. Newman. Simon and Schuster 1956.
THE FABRIC OF THE HEAVENS: THE DEVELOPMENT OF ASTRONOMY AND DYNAMICS. Stephen Toulmin and June Goodfield. Harper and Row, 1961.
AN INTRODUCTION TO THE THEORY OF NUMBERS. Fifth edition. G. H. Hardy and E. M Wright. Clarendon Press, 1978.
LITTLEWOOD'S MISCELLANY. Edited by Bela Bollobas. Cambridge University Press, 1986.
LURE OF THE INTEGERS. J. Roberts. Mathematical Association of America, 1992.
PROJECTS IN SCIENTIFIC COMPUTATION. Richard E. Crandall. TELOS/Springer- Verlag, 1994