Into the Eleventh Dimension

The quest for a theory linking all matter and all forces led physicists deep into hyperspace, where they got horribly lost. But suddenly the way ahead has become clear, says superstring theorist.

Michio Kaku

Is there a Final Theory in physics? Will we one day have a complete theory that will explain everything from subatomic particles, atoms and supernovae to the big bang? Einstein spent the last 30 years of his life in a fruitless quest for the fabled unified field theory. His approach has since been written off as futile.

In the 1980s, attention switched to superstring theory as the leading candidate for a final theory. This revolution began when physicists realised that the subatomic particles found in nature, such as electrons and quarks, may not be particles at all, but tiny vibrating strings.

Superstring theory was a stunning breakthrough. It became one of the fastest growing and most exciting areas of theoretical physics, generating a feverish outpouring of thousands of papers. Then, in the early 1990s, progress seemed to grind to a halt. People became discouraged when they failed to find the answers to two key questions: where do strings come from, and is our Universe among the many solutions of superstring theory? But now the Internet is buzzing again as papers pour in to the bulletin board at Los Alamos National laboratory in New Mexico, the official clearing house for superstring papers.

The trigger for this excitement was the discovery of "M-theory", which may answer those two vital questions about superstrings. "I may be biased on this one, but I think it is perhaps the most important development not only in string theory, but also in theoretical physics at least in the past two decades," says Harvard physicist Cumrun Vafa. M-theory led John Schwarz of Caltech, one of the founders of superstring theory, to proclaim a "second superstring revolution". And it inspired a spellbinding three-hour lecture by another leading exponent,Edward Witten of the Institute for Advanced Study at Princeton, New Jersey. The aftershocks of the breakthrough have spread to other disciplines, too. "The excitement I sense in the people in the field and the spin-offs into my own field of mathematics...have really been quite extraordinary," says Phillip Griffiths, director of the Institute for Advanced Study." I feel I've been very privileged to witness this first hand."

In one dazzling stroke, M-theory has come close to solving superstring theory's two long-standing questions , leaving many theoretical physicists (myself included) gasping at its power. M-theory, moreover, may even force string theory to change its name because, although many features of M-theory are still unknown , it does not seem to be a theory purely of strings. Other strange beasts seem to emerge, including various types of membranes. Michael Duff of Texas A&M University is already giving talks with the title " The theory formerly known as strings".

"Nature shows us only the tail of the lion. But I do not doubt that the lion belongs to it even though he cannot at once reveal himself because of his enormous size" - Albert Einstein

M-theory does not prove the final correctness of superstring theory. Not by any means. Proving or disproving its validity may take years more. But it still marks an astonishing breakthrough. Remember that some of the finest minds of this century have been stumped by the problem of creating a "Theory of Everything". Einstein summed up the problem when he said: Nature shows us only the tail of the lion. But I do not doubt that the lion belongs to it even though he cannot at once reveal himself because of his enormous size." The tail" is what we see in nature , which can be described by the four fundamental forces -gravity, electromagnetism and the strong and weak nuclear forces. The lion is the ultimate theory that will unify them in one short equation.

Today, physicists believe that the first force, gravity, can be described by Einstein's general relativity, based on the smooth warping of the fabric of space- time. This is an elegant theory that describes the macroscopic world of black holes, quasars and the big bang. But gravity has stubbornly refused to unite with the other three forces , which are described by quantum theory. Here, instead of the smooth fabric of space-time, we have the discrete world of packets of energy, or quanta.

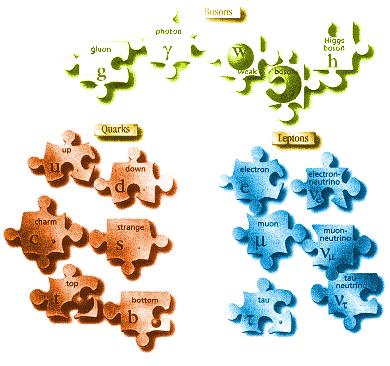
The form of quantum theory that goes furthest in describing matter and its interactions is the Standard Model, which is based on a bizarre bestiary of particles such as quarks , leptons and bosons (see Diagram). The Standard Model may be one of the most successful theories in science, but it is also one of the ugliest. Its inadequacy is betrayed by some 19 arbitrary constants not derived by any kind of theory that have to be put in "by hand" to make the equations work.

Capturing the "lion", which unites these two great theories, would be a crowning achievement for physics. But while Einstein was first to set off on this noble hunt, tracking the footprints left by the lion, he ultimately lost the trail and wandered off into the wilderness.

Crazy departure
Today, however, physicists are following a different trail-the one leading to superstring theory. Unlike previous proposals, it has survived every blistering mathematical challenge ever hurled at it. Not surprisingly, the theory is a radical-some might say crazy-departure from the past, being based on tiny strings vibrating in 10-dimensional space-time.

"The subatomic particles we see in nature are nothing more than different resonances of the vibrating superstrings"

To understand how going to higher dimensions can help to unify lower dimensions, think back to how the Romans used to fight wars. Without radio communications and spy planes, battles were horribly confused, raging on many fronts at the same time. That's why the Romans always leapt into "hyperspace"- the third dimension-by seizing a hill- top. From this vantage point, they were able to survey the two-dimensional battlefield as a single, unified whole.

Missing: the Standard Model works well, but still has big gaps. Could superstrings complete the picture?

Leaping to higher dimensions can also simplify the laws of nature. In 1915, Einstein changed completely our notion of gravity by leaping to the extra dimension of time. In 1919, the German mathematician Theodor Kaluza added a fifth dimension and in so doing unified space-time with Maxwell's equations for electromagnetism. This triumph was largely forgotten amid the frenzy of interest generated by quantum mechanics. Only in the 1980s did physicists return to this idea to create superstring theory.

In superstring theory, the subatomic particles we see in nature are nothing more than different resonances of the vibrating superstrings, in the same way that different musical notes emanate from the different modes of vibration of a violin string. (These strings are very small-of the order of 10³⁵ metres.)
Likewise, the laws of physics -the forces between charged particles, for example-are the harmonies of the strings; the Universe is a symphony of vibrating strings. And when strings move in 10-dimensional space-time, they warp the space-time surrounding them in precisely the way predicted by general relativity. So strings simply and elegantly unify the quantum theory of particles and general relativity. Better still, gravity is not an inconvenient add-on. "Unlike conventional quantum field theory, string theory requires gravity," Witten has said. "I regard this fact as one of the greatest insights in science ever made."

But, of course, all this takes place in 10 dimensions. Physicists retrieve our more familiar 4-dimensional Universe by assuming that, during the big bang, 6 of the 10 dimensions curled up (or "compactified") into a tiny ball, while the remaining four expanded explosively, giving us the Universe we see. What has consumed physicists for the past ten years is the task of cataloguing the different ways in which these six dimensions can compactify. Their task has been especially difficult because mathematicians have not worked out the topology and properties of these higher-dimensional universes. The physicists have had to blaze the trail and invent entirely new areas of mathematics. These efforts have revealed millions of compactifications, each of which yields a different pattern of quarks, electrons and so on.

As we have seen, the first frustrating problem with superstring theory is that physicists do not understand where strings come from. To make matters worse, there are five string theories that unify quantum theory with relativity. This is an embarrassment of riches. Each competing theory looks quite different from the others. One, called Type 1 string theory, is based on two types of strings : "open strings", like short strands with two ends, and "closed strings", in which the ends meet to form a ring. The other four have only closed strings. Some, such as Type 2b, generate only left- handed particles, which spin in only one direction [Ref I.Asimov "Left Hand of the Electron"]. Others, such as Type 2a, have left and right-handed particles.

Today's excitement has grown from the finding that if we postulate the existence of a mysterious M-theory in 11 dimensions we can show that the five competing string theories are actually different versions of the same thing. Like a Roman general surveying the battlefield from the third dimension, physicists today stand on the hilltop of the 11th dimension and see the five superstring theories below, unified into a simple, coherent picture, representing different aspects of the same thing.

Tracking lion
The first step towards this advance came two years ago when Witten and Paul Townsend of the University of Cambridge showed that Type 2a string theory in 10 dimensions was equivalent to M-theory in 11 dimensions with one dimension curled up. Since then, all five theories have been shown to be equivalent. So at last physicists know where superstrings come from : they originate in the 11th dimension from M-theory.

M-theory also predicts that strings coexist with membranes of various dimensions. For example , a particle can be defined as a zero-brane (zero-dimensional object). A string is a one-brane, an ordinary membrane like a soap bubble is a two-brane, and so on. (Using p to represent the dimension of the object, one wag dubbed this motley collection "p-branes" ) When these p-branes vibrate or pulsate , they create new resonances , or particles, which were missed in earlier formulations of superstrings. The name "M-theory" was coined by Witten: M perhaps stands for "membrane" or the "mother of all strings", or possibly "mystery" Take your pick.

To see how this all fits together, imagine three blind men hot on the trail of Einstein's lion. Hearing it race by, they give chase and desperately grab at it. Hanging onto the tail for dear life, one feels its one-dimensional form and loudly proclaims, "It's a string. The lion is a string." The second man grabs the lion's ear. Feeling a two-dimensional surface , he calls out "No, no, the lion is really a two-brane." The third blind man, hanging on to the lion's leg, senses a three-dimensional solid, and shouts , "You're both wrong. The lion is a three- brane !" They are all right. Just as the tail, ear and leg are different parts of the same lion , the string and various p-branes appear to be different limits of M-theory. Townsend calls it "p-brane democracy".

The acid test for any theory is that it must fit the data. No matter how original and elegant superstring theory is , it will stand or fall on whether it describes the physical Universe. Either it is a Theory of Everything, as its advocates hope , or it is a theory of nothing. There is no in-between. So theoretical physicists must answer the second question : is our Universe, with its strange collection of quarks and subatomic particles, among the solutions of superstring theory? This is where it runs into an embarrassing problem, which is that physicists have been unable to find all its four-dimensional solutions. The mathematics have been fiendishly difficult-too hard for anyone to solve completely.

In general, there are two types of solutions. So far, only the first class, called "perturbative" solutions have been found. Across all branches of physics, theorists faced by an equation they cannot solve reach for well-established ways to find approximate solutions. In superstring theory, millions of these perturbative solutions have been catalogued. Each one corresponds to a different way in which to curl up 6 of the 10 dimensions. However, none of them precisely reproduces the pattern of quarks , leptons and bosons in the Standard Model, although some come close.

"M-theory solves entire classes of problems that were previously thought to be unsolvable . It even gives us valuable details of quantum effects In black holes"

So, many believe that the Standard Model may be found among the second class of solutions, the "non-perturbative" solutions. But non-perturbative solutions are generally among the most difficult of all solutions in physics. Some physicists despaired of ever finding non- perturbative solutions of superstring theory. After all, even the non-perturbative solutions of simple four-dimensional theories are completely unknown , let alone those of a complicated 10-dimensional theory.

How does M-theory help to solve this intractable problem? The answer lies in a startling tool called "duality". Simply put, in M-theory there is a duality, or simple mathematical relationship , between the perturbative and non-perturbative regions. This allows us at last to take a peek at this "forbidden zone".
To see how duality works, consider Maxwell's theory of electricity and magnetism , for example. Physicists have known for decades that if they interchange the electric field E and magnetic field B in Maxwell's equations , and also swap the electric charge e and magnetic charge g, then the equations stay the same. That is, nothing happens to Maxwell's theory if we make the dual transformation: E«B and e«g.

Hidden theories
In fact, in Maxwell's theory, the product e times g is a constant: so small e corresponds to large g. This is the key. Suppose an equation includes a mathematical function that depends on g² and which cannot be solved exactly. The standard mathematical trick is to approximate a solution with a perturbation expansion: g²+ g⁴ + g⁶... and so on. So long as g is less than 1, each successive term in the series is smaller than the last, and the overall value converges on a single figure.

But if g is greater than 1 then the total gets larger and larger, and the approximation fails. This is where duality comes in. If g is large, then e is less than 1. Using perturbation , we get the series e²+ e⁴ + e⁶ which gives a sensible value. Ultimately, this means that using perturbation on e can solve problems in the non-perturbative region of g.

Duality in Maxwell's theory is rather trivial. But in M-theory, we find another duality: g«1/g. This relationship, though simpler, turns out to be incredibly powerful. When I first saw it, I could hardly believe my eyes. It meant that a string theory defined for large g, which is usually impossible to describe using present-day mathematics, can be shown to be equivalent to another type of string theory for small g, which is easily described using perturbation theory.

Thus, two different string theories can be dual to each other. In the non- perturbative region of string theory was another string theory. This is how, in fact, we prove the equivalence of all five string theories. Altogether, three different types of duality called S, T and U have been discovered , which yield an intricate web of dualities linking string theories of various dimensions and types. At an incredible pace , physicists have now mapped almost all the solutions and dualities that exist in 10, 8 and 6 dimensions.

Before M-theory, finding the non-perturbative solutions in these dimensions would have been considered impossible. Now the problem is trivial. For example , let us say that two theories A and B are dual to each other in 10 dimensions. If we compactify both theories in the same way, then we obtain theories A' and B'. But now we know something new: that A' is also dual to B'. Thus, the non-perturbative behaviour of A' is given by B'. By elaborating this process, we get an almost complete understanding of the different possible universes down to 6 dimensions. Thus, M-theory solves entire classes of problems that were previously thought to be unsolvable. It even gives us valuable new details about quantum effects in black holes.

But there are many loose ends. For example, what precisely is M-theory? So far, we only know fragments of the theory (the low-energy part). We are still waiting for someone to come up with a full description of M-theory Last year, Vafa shocked physicists by announcing that there may be a 12-dimensional theory lurking out there, which he called "F-theory" (F for father).

More important, we are still far from mapping all the dualities of four dimensions. If everything works out as hoped , we should find that one of these four- dimensional universes contains the Standard Model and thus describes the known Universe. But there are millions of these solutions, so sifting through them to find the one we are after will take many years.

So will the final theory be in 10, 11 or 12 dimensions? According to Schwarz, the answer may be none of these. He feels that the true theory may not have a fixed dimensionality, and that 11 dimensions only emerge once we try to solve it. Townsend takes a similar view, saying, " The whole notion of dimensionality is an approximate one that only emerges in some semiclassical context."

So does this means that the end is in sight-that some day soon we will be able to work out the Standard Model from first principles? When I put this question to some leading physicists in this field they were still cautious. Townsend likened our present state of knowledge to the old quantum era of the Bohr atom, just before the full elucidation of quantum mechanics. "We have some fruitful pictures and some rules," he says. "But it's also clear that we don't have a complete theory."

Witten, too, believes we are on the right track. But he says we will need a few more "revolutions" like the present one to finally solve the theory. "I think there are still a couple more superstring revolutions in our future, at least," says Witten. "If we can manage one more superstring revolution a decade , I think that we will do all right." From Harvard, Vafa adds: "I hope this is the light at the end of the tunnel'. But who knows how long the tunnel is?"
Personally,I am optimistic. For the first time, we can see the outline of the lion , and it is magnificent. One day, we will hear it roar.

Author

Michio Kaku is professor of theoretical physics at the City University of New York and author of Hyperspace: A Scientific Odyssey through the 10th Dimension, Oxford University Press.