 |
Shadows from Higher Dimensions
|
Ivars Peterson
For many dabblers in geometry, the doorway to higher dimensions has been a slim volume called Flatland. The book's central figure and narrator, "A Square," takes his readers into a two-dimensional world where a race of rigid geometric forms live and love, work and play. Like shadows, the denizens of Flatland freely flit about on the surface of their world but lack the power to rise above or sink into it. All Flatland's creatures - straight lines, triangles, squares, pentagons, and higher figures-are trapped in their planar geometry (Figure 4.1).
FLATLAND AND BEYOND
On the surface, Edwin A. Abbott's narrative, written more than a century
ago, appears simply to be a good story and a clever mathematics lesson. Although
their real shapes are two-dimensional, Flatlanders appear to one another
as straight lines. Residents of a three- dimensional world see the reason
for a Flatlander's limited vista.
 |
| FIGURE 4.1 The title page from the first edition of Flatland, published in 1884, hints at the book's whimsical nature. |
Viewed from above, a coin sitting on a table clearly looks circular. As the
angle of view shifts closer to the plane of the table, the coin looks more
like an oval. At Flatlander level, along the table's surface, the oval thins
to nothing more than a straight line. Using such examples in Flatland,
Abbott neatly introduces key ideas in projective geometry and illustrates
other important mathematical concepts.
Flatland is also a pointed satire that reflects widely debated social
issues of Victorian Britain. Abbott was a strong advocate of
women's rights who couldn't resist taking a satirical
swipe at his society's attitudes toward women. Flatland women are merely
Straight Lines. Lower-class men are Isosceles Triangles; Squares make up
the professional class; Nobles are polygons with six or more sides; and Priests,
the highest-ranking members, are perfect Circles.
"[A] Woman is a needle; being, so to speak, all point, at least at the two
extremities," says "A Square," the scholarly commentator. "Add to this the
power of making herself invisible at will, and you will perceive that a Female,
in Flatland, is a creature by no means to be trifled with." Nevertheless,
Flatland women also are "devoid of brain-power, and have neither reflection,
judgment nor forethought, and hardly any memory." In this planar world, men
believe that educating women is wasted effort and that communication with
women must be in a separate language that contains
"irrational and emotional conceptions" not otherwise
found in male vocabulary.
When he wrote Flatland, Abbott was headmaster at the City of London
School, an institution that prepared middle-class boys for professional careers
and for places at universities such as Cambridge. He produced dozens of books,
including school textbooks, historical and biblical studies, theological
novels, and a well-regarded Shakespearean grammar
that strongly influenced the study of the Bard's
plays. At first, Flatland seems out of place within this collection,
but a closer look shows that it combines elements from Abbott's broad range
of interests, from the nature of miracles to the reform of mathematics education.
Abbott was part of a group of progressive educators who sought changes in
the mathematics requirements for university entrance, which at that time
included the memorization of lengthy proofs in euclidean geometry. Abbott's
group considered such an exercise a waste of time and felt it narrowed the
study of geometry unnecessarily.
Despite Abbott's views and the growth of popular interest in concepts of
a fourth dimension and even higher dimensions, the conservative mathematics
establishment in Britain prevailed. Establishment mathematicians refused
to admit that higher-dimension geometries were even conceivable, maintaining
that such concepts would call into question the very existence and permanence
of mathematical truth, as represented by three-dimensional euclidean geometry
[Ref: Reimann/Lobachevsky]. Abbott challenged the establishment and deliberately
called Flatland's university "Wentbridge" -a sly dig at Cambridge.
Flatland also represents one of Abbott's attempts to reconcile scientific
and religious ideas and to clarify the relationship between material proof
and religious faith. In one episode, "A Square" receives a visit from
a ghostly sphere, who tries to demonstrate to the bewildered Flatlander the
existence of Spaceland and a higher dimension. The visiting sphere argues
that he is a "Solid" made up of an infinite number of circles, varying in
size from a point to a circle 13 inches across, stacked one on top of the
other. In Flatland, only one of these circles is visible at any given time.
Rising out of Flatland, the sphere looks like a circle that gets smaller
and smaller until it finally dwindles to a point, then vanishes completely
(see Figure 4.2).
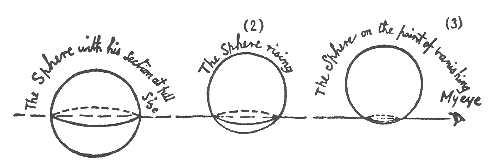 |
| FIGURE 4.2 To a Flatlander, a Sphere passing through Flatland appears as a circle of changing diameter. |
When that demonstration fails to persuade "A Square" that the sphere is truly
three-dimensional, the visitor tries a more mathematical argument. A single
point, being just a point, he insists, has only one terminal point. A moving
point produces a straight line, which has two terminal points. A straight
line moving at right angles to itself sweeps out a square with four terminal
points. Those are all conceivable operations to a Flatlander. Inexorable
mathematical logic forces the next step. If the numbers 1, 2, and 4 are in
a geometric progression, then 8 follows. Lifting a square out of the plane
of Flatland ought to produce something with eight terminal points. Spacelanders
call it a cube. The argument opens a path to even higher dimensions.
Through mathematical analogy, Abbott sought to show that establishing
scientific truth requires a leap of faith and that, conversely, miracles
can be explained in terms that don't violate physical laws. Like early scientific
theories, miracles could be merely shadows of phenomena beyond everyday
experience or intrusions from higher dimensions. Flatland raises the
fundamental question of how to deal with something transcendental, especially
when recognizing that one will never be able to grasp its full nature and
meaning. It's the kind of challenge that pure mathematicians face
when they venture into higher dimensions. How do mathematicians organize
their insights? How do they see and understand multidimensional worlds? How
do they communicate their insights? Flatland is a novel approach toward answering
those questions.
