A weather eye on unpredictability

Much of chaos theory came from trying to understand how the Earth's atmosphere behaves. Now,meteorologists are using chaos to assess how reliable climate and weather forecasts are .

Tim Palmer

EVERY DAY, meteorologists try to predict next week's weather using immensely complicated mathematical descriptions of how the atmosphere behaves. Research is also under way to develop models that will help them make predictions on an even longer timescale, seasonal forecasts of monsoon rains, for example. Meteorologists would even like to be able to estimate changes in climate resulting from human activities, such as the greenhouse effect.

And yet we know that the atmosphere is a chaotic system. As such, it is inherently unpredictable (see Box). So, are these attempts at longer-range weather and climate prediction a waste of time? Should we content ourselves with the television forecast of tomorrow's weather, and leave the rest to chance?

Although the weather can change every day as individual systems progress eastwards, depressions and their associated weather fronts, for example, certain spells of weather can last for weeks, months or even whole seasons. These spells are not characterised by individual weather systems, but by the position of the so-called jet streams, regions of strong wind in the upper atmosphere. They determine whether we will have a wet or dry summer, mild or severe winter.

Chaos and high winds across the planet THE SUN'S energy and Newton's laws are responsible for chaos in the atmosphere. Sunlight warms the tropical regions of the Earth, whilst over the poles, heat energy is radiated back to space, and there the atmosphere cools. The atmosphere attempts to pump heat from equator to pole in as thermodynamically efficient a manner as possible. If the Earth were not rotating about its axis, the most efficient way of transporting this heat would be as follows: air heated at the Earth's surface in the tropics would rise in tropical latitudes, flow towards the poles in the upper atmosphere, sink over the poles, and return to the tropics in the lower atmosphere. This overturning motion across the planet would happen at all longitudes. In practice, it happens only in tropical and subtropical latitudes (with the large-scale sinking of air in the subtropics, giving rise to the desert regions of the Earth). In middle and high latitudes, the effects of the Earth's rotation on the dynamics of the atmosphere become important, giving rise to the so-called Coriolis effect, whereby projectiles tend to curve to the right in the northern hemisphere relative to an observer on the ground. As a result of the Coriolis effect, it is thermodynamically efficient to flux heat energy towards the poles through the depressions and anticyclones that we call weather systems. Mathematically, we can describe these weather systems as fluid-dynamical instabilities of a spherical shell of rotating fluid, which is heated over the equator and cooled over the poles. Theory correctly predicts the scale of these instabilities, about 1000 kilometres, with rates of growth corresponding to an amplitude doubling in a couple of days or so. The weather systems also flux momentum into middle latitudes from the tropics. This flux of momentum maintains the prevailing westerly winds against frictional dissipation at the Earth's surface. The westerly winds increase with height to a maximum in the so-called jet streams. The positions of the jet streams are not fixed in space and time, but meander, over distances of about 10000 kilometres, longer length-scales than those associated with individual weather systems (see Figure 1). The positions of the jet streams can be used to define large-scale weather regimes; those determining the general pattern of weather experienced, say, during a period of a week or more, settled or unsettled, for example. Although individual weather systems are instabilities of the larger-scale flow, they play a major role in maintaining the meanders of the jet stream on a planetary scale. From a mathematical point of view, this feedback between individual weather system instabilities and the larger-scale flow is a nonlinear process. Forced by the heat energy of the Sun, the atmosphere is, therefore, unstable and nonlinear. These two characteristics are the crucial components for chaos. The evolution of a chaotic system is sensitive to the precise specification of the initial state; this means that irrespective of how complex our models become, or how accurate our weather data are, the laws of science impose a limit beyond which prediction of the weather is impossible.

Figure 1 shows the track of the jet stream over the Atlantic and Europe, which is associated with two different weather "regimes". In Figure la, the jet stream is more or less oriented along a line of latitude. Individual weather Systems tend to be steered along the jet stream. Over the British Isles, this configuration would probably give a rather wet and unsettled spell of weather, as rain bands pass by with monotonous regularity. Meteorologists call this a "zonal" regime. In Figure lb, the jet stream splits into two branches over the mid-Atlantic, with one branch positioned north of the British Isles, the other to the south. In the summer, this configuration brings about a warm fine spell of weather over Britain; in the winter, it produces dull, overcast, and possibly very cold weather. Meteorologists usually refer to this as a "blocked" regime.

We can define weather regimes quantitatively from historical records of data of weather in the northern hemisphere, using what are called "cluster-analysis" techniques. In practice, about 10 different regimes characterise most of the large-scale variability of the atmosphere in the northern hemisphere.
Meteorologists have been interested for a long time in the predictability of these weather regimes. Can we forecast how they evolve up to a month ahead, even though we can predict what happens to individual weather systems for only a few days ahead?

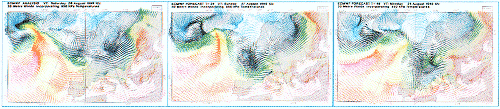These complex maps from the ECMRWF computer model show predicted weather patterns for six days. Arrows show wind direction and colour (blue: cold; red: warm) shows temperature.

These sort of problems motivated the meteorologist Edward Lorenz, whose work at the Massachusetts Institute of Technology in the early 1960s spawned much of the activity in chaos theory today. The atmosphere behaves like a turbulent fluid, and Lorenz was only too aware that it was governed by a set of mathematical equations that were nonlinear and were extremely sensitive to small changes-in other words, showed modes of instability. He had an intuitive feeling that this would make weather prediction a tough problem. To confirm his hunch, he sought a way of simplifying these equations so that he could study them mathematically, while retaining their essential nonlinearity and instability.

The most drastically simplified version of the full fluid-dynamical equations led to a "model climate" with just three variables, x, y and z. A state of instantaneous "weather" in Lorenz's model can, therefore, be represented by a point in a three-dimensional "phase space" and the evolution of the weather with time can be represented by a line, or trajectory, in this space (as described in Ian Stewart's article "Portraits of chaos", New Scientist, 4 November). The climate of the model, the set of all possible model weather states, is known as the Lorenz attractor (see Figure 2).

Figure 1 The position of the jet stream over Europe and the Atlantic in two weather regimes. The first gives rather unsettled weather over the British Isles; the second may give fine warm weather in the summer, dull and possibly severely cold weather in the winter.

This attractor has no volume in this three-dimensional space, yet is neither a simple one-dimensional line, nor a smooth two-dimensional surface. As Ian Stewart's article explains, the attractor has a fractional dimension (2.06), and therefore, not surprisingly, carries the epithet "strange". It represents one of a generic class of strange attractors whose topology characterises the chaotic, unpredictable properties of the basic equations.

Although the three-component equations that Lorenz proposed do not realistically describe the evolution of weather regimes, they have similar chaotic properties to more realistic models. So we can use the Lorenz model to describe in a qualitative way the chaotic behaviour of the evolution of weather regimes in the atmosphere.
First, notice from Figure 2 that the Lorenz attractor has two separate branches, sometimes called butterfly wings. We can think of these wings as representing, in our abstract state space, the two weather regimes shown in Figure 1 in real space. For the sake of argument, suppose the left-hand wing corresponds to the zonal regime of Figure la, and the right hand wing corresponds to the blocked regime of Figure lb. In other words, any two points on the left-hand wing relate to different instantaneous weather, but the large-scale flow would be the same.

Imagine two points arbitrarily close to each other, on the left-hand wing of the attractor. Using our conventions, these two points represent almost identical weather states in a regime characterised by rather unsettled weather conditions over the British Isles.We now follow the initial evolution of these two weather states. There are three possibilities: both trajectories remain on the left-hand wing (see Figure 3a); both trajectories evolve towards the right-hand wing, as in Figure 3b; or one trajectory remains on the left-hand wing, while the other moves to the right-hand wing, as in Figure 3c. Note that in all three cases, the two trajectories have diverged, implying quite different forecasts of instantaneous weather. On the other hand, in the first two scenarios (see Figures 3a and 3b), the two trajectories evolve to the same weather regime (remaining unsettled in the first case; becoming more settled in the second case).

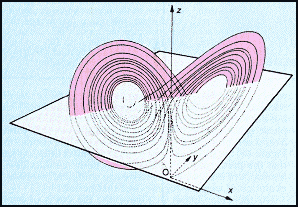Figure 2 The Lorenz attractor in the three-dimensional phase space spanned by the Lorenz model variables x, y, z.

You can see, therefore, that although the atmosphere is fundamentally chaotic, you can predict the weather regime from certain initial conditions in the atmosphere. To find out what these initial conditions are, we need to make a series of weather forecasts from (a sufficiently large number of) similar but not identical initial states. Figure 4 shows the evolution in phase space of two ensembles of realistic weather forecasts over a certain period. For the first set of initial conditions, in Figure 4a, the forecasts start to diverge only a little, indicating that the predictability for that set of initial conditions in the atmosphere is pretty good, so we can confidently forecast the evolution of weather regime over that period.

On the other hand, in Figure 4b, the paths of evolving weather patterns from similar initial conditions disperse considerably, indicating that the atmosphere is in a particularly chaotic state during the period of the forecasts, so we cannot make any meaningful predictions.
Now, the Lorenz model has only three variables, or three degrees of freedom. It is much too simple to describe accurately the evolution of the real atmosphere. In fact, increasing the number of degrees of freedom in models has improved the quality of weather-prediction for the first few days ahead. Today's weather-prediction models have about a million degrees of freedom.

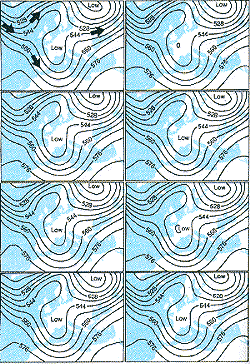
Figures 5 and 6 show an example of an ensemble of eight forecasts from the weather prediction model we use at the European Centre for Medium-Range Weather Forecasts (ECMWF). The pictures show contours of the height of a pressure surface (500 hectopascals) in the middle of the atmosphere. The wind blows parallel to these contours in the direction shown by the arrows-the strength of the wind is proportional to the contour gradient. Figure 5 shows the initial conditions for the eight forecasts. Note that they look very similar.
Differences between individual members of the ensemble correspond to uncertainties associated with the weather observing network. The initial flow in Figure 5 corresponds approximately to the pattern shown in Figure 1; over Britain, the flow is very weak, with the region of strong winds splitting over the east Atlantic towards the north-east and south-east.

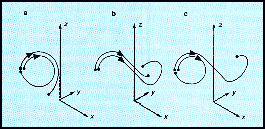Figure 3 Three trajectories showing the evolution in Lorenz's model atmosphere from almost identical weather states. In a and b, the states evolve similarly; in C, they evolve differently.

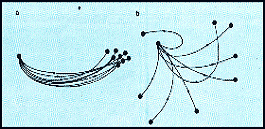Figure 4 The evolution of an ensemble of forecast trajectories in the phase space of a realistic model for weather prediction. In a, we can give the forecast with confidence, but not so in b.

We now run the computer model eight times from each of these initial conditions and see what the model predicts for the weather one week later. This is shown in Figure 6. You can see that the forecasts are now far from identical; their trajectories in phase space (not shown) have begun to diverge significantly. However, over some parts of Europe, you can see a weather pattern common to many of the members of the ensemble. Over Italy, for example, the initial state showed an air flow from the south; after a week, the winds swing round so that they have a northerly component. So, an Italian forecaster could confidently predict that Italy should expect much colder weather a week ahead. Using the ensemble, the forecaster could estimate probabilities that temperature will fall within certain ranges.

By contrast, the British weather forecaster would have a more difficult task-the forecasts over Britain diverge much more (confirming the saying about the unreliability of British 'weather). Nevertheless, it would not be unreasonable to predict a trend to more westerly flow and unsettled weather. This example is one that is neither particularly chaotic, nor exceptionally predictable, and highlights the practical consequences of chaos for the weather forecaster.
There are many research centres around the world exploring the possibility of predicting the evolution of weather regimes up to a month ahead. It is early days in this business, and meteorologists still need to refine their description of various important physical processes in the computer models. If they are to forecast weather regimes this far ahead, they will have to run ensemble forecasts of the sort just described, so as to be able to estimate how reliable the prediction is. At present, raw computing power is still insufficient to do this routinely. But with advances in computer technology, this kind of forecasting may not be many years away.

So far, we have talked about weather in the middle latitudes. In the tropics, the dynamics of the atmosphere is somewhat different, mainly because the Coriolis effect of the Earth's rotation is less dominant. In particular, although there are weather systems in the tropics, such as hurricanes, monsoon depressions and so on, that arise from instabilities of the larger-scale flow, these weather systems do not feed back into the larger-scale flow to the same extent as with weather systems in the middle latitudes. In fact, the behaviour of the large-scale tropical atmosphere is very strongly linked to the temperature of the ocean surface, which evolves over months, rather than days. One well-studied phenomenon that intimately involves the coupled dynamics of the ocean-atmosphere system is the so-called El Niño event, during which ocean temperatures in the tropical east Pacific can rise up to 4 °C above normal during a season. Meteorologists believe that El Niño can influence weather patterns over a substantial fraction of the globe.

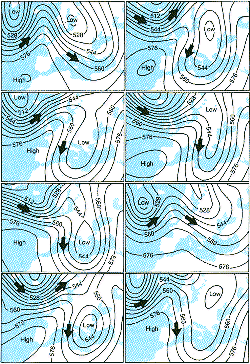Figure 5 Initial conditions for eight forecasts of the weather prediction model of the European Centre for Medium-Range weather Forecasts.Arrows show the direction of the wind.	Figure 6 Predictions one week later for the eight forecasts. The ensemble shows that we can predict the weather for Italy with more confidence than we can for Britain.

It may be feasible to predict flow on a planetary scale in the tropical atmosphere for a season, using models that take into account the dynamics of both the atmosphere and the oceans. Certainly there have been some encouraging successes in forecasting El Niño and its consequences a season ahead. In a few years' time, weather forecasters may be able to predict seasonal rain over Africa, India and other tropical countries from such weather prediction models. However, nonlinearity and instability, the hallmarks of chaos, are not totally absent in these tropical predictions, and it is likely that the "multiple-ensemble integrations" which people have already applied to weather at mid-latitudes will still be a necessary tool for the tropical forecaster.

Finally, does chaos theory prevent us from predicting possible climate change in the next century? The answer here is no. The type of prediction is quite different from that outlined above. Here, the goal is not predicting an individual trajectory on the climate attractor; the goal is to determine the shape and position of the whole climate attractor itself when, for example, greenhouse gases increase.
The critical question that climatologists are trying to answer is whether the climate attractor will suffer a minor perturbation (for example, small shift of the whole attractor along one of the axes of phase space), or whether there will be a substantial change in the whole shape and position of the attractor, leading to some possibly devastating weather states not experienced in today's climate. Chaos theory certainly does not forbid the possibility of some substantial change to the atmosphere's climate attractor as a result of modest increases in the amount of carbon dioxide. At the moment, we cannot be sure of the answer. The same sort of models employed in predicting the weather are also being used to try to find out what the greenhouse effect has in store for us. As with attempts at predicting weather regimes, uncertainty in climate forecasting is mitigated by the fact that several of the climate centres around the world now have sophisticated models. Again, researchers can evaluate their confidence in predicting greenhouse warming in terms of the dispersion of the ensemble of predictions from these different models.

Nevertheless, chaos dynamics should caution us from making too premature a judgment about climatic changes. Returning to the Lorenz attractor, there is no pre-ordained number of times that a given trajectory must circle around one of the butterfly wings; it could be once, 10 times, or 100 times, depending on the precise position of the trajectory on the attractor. If we have a mild winter, a warm summer, then another mild winter, we might not necessarily be in the throes of man-made climate change; the system might just be revolving happily around one small part of phase space, and on that hundred and first revolution, the system might, quite unexpectedly, and for no apparent reason, evolve towards another part of phase space, which is associated with cold winters and miserable summers. For this reason, many meteorologists are quite guarded about whether global warming due to the greenhouse effect really has arrived.

To the lay person, the unpredictability of the weather may be a curse; to the meteorologist, it is what makes the subject fascinating, and fun to study. Above all, chaos does not mean that we must throw in the towel, and leave all to chance. This blend of fundamental science with state-of-the-art computer technology is leading to unparalleled insights into the workings of the fragile gaseous envelope that surrounds and sustains us.

Tim Palmer is head of the predictability and diagnostics section of the European Centre for Medium-Range Weather Forecasts in Reading, Berkshire.

Further Reading Predictability in Science and Society, John Mason, Peter Mathews and J. H. Westcott (editors), Cambridge University Press, 1984; Topics in Geophysical Fluid Dynamics: atmosphere dynamics, dynamo theory, and climate dynamics, H. Ghil and S. Childress, Applied Mathematical Sciences, volume 64, Springer Verlag, 1987. Next week: Robert May explains how chaos arises in population dynamics, natural selection and physiology.

MAIN INDEX
REFERENCE GUIDE			TRANSCRIPTS				GLOSSARY
Chaos	Quantum	Logic	Cosmos	Conscious	Belief	Elect.	Art	Chem.	Maths